(1) Take two things, A and B, and Merge them to form a new thing, C.
(2) Give C the label of either A or B.
(3) Repeat as necessary.
This is the algorithm of Bare Phrase Structure. To give a concrete example, here's how you might construct a prepositional phrase like [under the green table]:
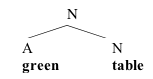
(i) Merge green and table, projecting the label of table to the new constituent:

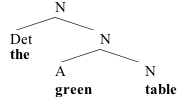
(ii) Merge the and green table, projecting the label of green table:
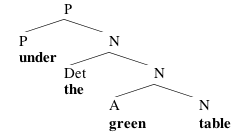
(iii) Finally, Merge under, projecting the label of under:
Now, in the above trees, I haven't distinguished between nodes with the same label; there aren't any NPs or N's here. Like most syntacticians, I actually find that Ps and 's make trees easier to process, so I'll add them. But it's worth emphasizing that these aren't supposed to have any real status as part of the syntactic representation; they're just there to make trees easier to read. You can add them using the following convention:
(4) Given a sequence of nodes with the same label X in immediate dominance relations with each other:
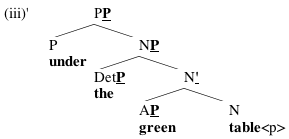
The convention underdetermines how we ought to treat things like green and the in this tree, which are both the highest and the lowest nodes in their (very short) sequences; we could equally well call green an A or an AP, for example. Feel free to do whatever you want.
Bare Phrase Structure is part of a movement in syntax called Minimalism, which emphasizes getting by with a bare minimum of syntactic apparatus. It's clear that we have to create trees that consist of phrases; the facts don't give us any way out of that. The simplest way to create complex objects out of simple objects is (arguably) to take two simple objects and put them together to form a new object, and just keep doing that until you're done. This is (almost) the only kind of operation used here. The only other component of the algorithm in (1-3) is projection of labels; again, the facts seem to demand labels, so the simplest way of applying them is just to use the label of one of the objects we're manipulating (of course, there are other things you could imagine doing, like always giving the same label to everything, but none of them seem to cover the facts very well).
This approach to tree building allows us to have intermediate levels of structure, smaller than XP but larger than X. We decided we wanted that, for two reasons. Consider (iv):
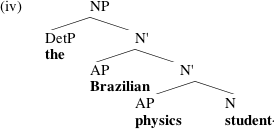
We've decided that Brazilian is an adjunct, and physics is a complement; that is, Brazilian is the kind of adjective that could modify almost anything (Brazilian doctor/lawyer/invention/law/history...) whereas physics can only combine with a fairly small set of nouns (physics student/professor/textbook/class), and is therefore arguably selected by the head N student (that is, this N is listed in the lexicon as optionally taking a complement indicating the field of study). The syntactic distinction between complements and adjuncts is represented by a condition requiring complements to be sisters of the head that selects them; adjuncts, by contrast, can in principle go anywhere.
These conditions allow us to distinguish between (iv) and the ill-formed (v):
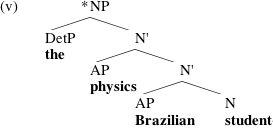
We correctly predict that complements will have to be closer to the head than adjuncts; in (v), the complement physics fails to be a sister of the selecting head N.
For historical reasons, you should also know about X-bar theory, which resembles Bare Phrase Structure in that it replaces the very specific phrase structure rules that we saw at the beginning with a more general template (one which, like the Bare Phrase Structure theory, allows for intermediate bar levels); this is the theory that the optional Radford reading is discussing. The general template consists of three rules (order is irrelevant):
(5) XP→ (AP) X'
(6) X'→ (BP) X'
(7) X'→ (CP) X
These rules have the consequence that absolutely every head X must be dominated by at least one X', and on top of all the X's there is an XP. In the tree in (iv) above, for example, the projection of the head N conforms to the X-bar schema, but the DetP and the APs do not. To obey (5-7), the tree in (iv) would have to be changed to (iv'):
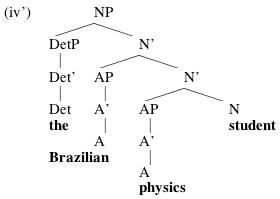
These nonbranching projections are forced by the X-bar theory, but they never seem to do us any good. Moreover, to those of us who are deeply enmeshed in Minimalist thinking, (5-7) seem a lot more arbitrary than Bare Phrase Structure. BPS basically says "You need a way of making complex structures out of atomic lexical items? Okay, take pairs of things and put them together to make bigger things, until you run out of things; then stop". The rules in (5-7) are a lot more specific than that, and hence more arbitrary; one could write equally simple rules that allowed projections to have two heads, or none.
Of course, because Bare Phrase Structure doesn't say much, the burden of making sure that labels project correctly and that heads take the right kinds of complements, etc. has to fall to other areas of the grammar. So far our focus has been on selection, which allows us to guarantee that (for instance) the verb imitate will have an NP complement, without having to write an independent phrase structure rule that specifically declares this to be an option for verbs.
And as we saw in class, we might hope that selection will sometimes take care of correct label projection, too. Suppose we're Merging the V imitate with an NP a walrus:
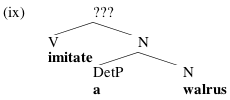
In principle, either V or N could project, giving you the possibilities in (x):
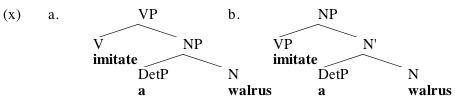
But there are clearly problems with (b): the verb imitate, which selects for an NP sister, doesn't have one, and the N walrus has an adjunct VP imitate, which is going to be ruled out by conditions on how adjuncts are interpreted. In principle, we could posit an algorithm that always explains which of two labels ought to project ("when Merging a V and an N, project the V..."), but given that independent principles seem to doom the wrong choice here, maybe we don't need to bother coming up with such an algorithm.
Now, as the Merge algorithm in (1-3) is stated, it produces only trees with binary branching; that is, every non-terminal node has exactly two daughters. We could have stated it differently, of course; for example, (1) could have started with "Take an arbitrary number of things..." But as things are stated, Merge takes exactly two things. This produces one immediate difference between the trees we've got now and the trees we were looking at before; we used to have a ternary-branching TP, as in (xi), but now we need TP to be binary-branching, as in (xii):
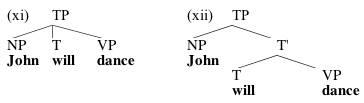
Is there any independent evidence for the binary-branching tree in (xii) over the ternary-branching one in (xi)? Well, one piece of evidence has to do with another (slightly shaky) constituency test, involving coordination. You can coordinate NPs with other NPs, for example; this involves putting the word and between them:
(8) John bought [an apple] and [a lemon]
And you can coordinate VPs:
(9) Mary [bought an apple] and [sold a lemon]
And, as you won't be surprised to hear by now, you can't just coordinate random strings of words:
(10) *John [bought a] and [sold a] lemon.
So coordination is a constituency test; if you can coordinate things, they're probably a constituent. Unfortunately, it's sort of a dangerous constituency test, because there are places where it seems to fail. For instance, (11) is fine:
(11) [John bought], and [Mary sold], a lemon.
(11) is an instance of something called Right Node Raising, which is very mysterious. Here the coordinated phrases seem to be John bought and Mary sold, which had better not be constituents, if the trees we're drawing are even vaguely right. So there's something complex going on here. Fortunately, we can sort of recognize Right Node Raising when we hear it; it has a special intonation, which is represented by the commas in (11), and which doesn't have to appear in examples like (8-9). The special intonation probably has something to do with the fact that the non-coordinated stuff in a Right Node Raising example can't just be a pronoun:
(12) *[John bought], and [Mary sold], it.
This isn't true of the non-coordinated stuff in ordinary coordination:
(13) she [bought an apple] and [sold a lemon].
Similarly, examples like (14) seem to involve coordination of nonconstituents (as was pointed out in class):
(14) John bought a record, and Mary a book
Examples like (14) are referred to as Gapping; here, again, we seem to be coordinating a nonconstituent, since there shouldn't be any constituent Mary a book that excludes the verb buy. One distinguishing characteristic of Gapping is that it requires the Gapped material to contrast with the preceding material; (14) is acceptable, but (15) isn't:
(15) *John bought a record, and Mary a record (too)
We could speculate that there's some process involved in the creation of Gapping examples like (14), which is connected somehow to this contrastive interpretation.
So perhaps we can try using coordination as a constituency test, bearing in mind that things like Right Node Raising and Gapping make it a dangerous test; apparently there are operations that can at least create the appearance of coordination of nonconstituents. As long as we're careful to only consider examples in which those operations aren't taking place (that is, as long as we're careful to avoid Right Node Raising and Gapping), we should be able to (cautiously) use coordination as a constituency test. So with that in mind, consider examples like (14):
(16) I [have won the lottery] and [will never work again]
For (16) to be well-formed, we need strings like have won the lottery and will never work again to be constituents. They are consistuents for the binary-branching tree in (xii), but not for the ternary-branching tree in (xi). So that's one argument that our algorithm for Merge is correct as stated.