Controlling Waves with Embedded Eigenvalues

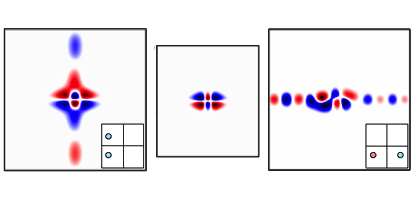
A BIC is a localized state embedded in a continuum of delocalized states. While BICs were first theoretically demonstrated in the radial equation by Von Neumann and Wigner in 1929, they were often seen as a mere mathematical curiosity. In my work, I showed a class of BICs which arises from the separability of the wave equation. I have demonstrated these BICs in photonic systems, quantum electronics, ultracold atom systems, and any wave system which can be modeled in the tight-binding approximation. Moreover, I showed that separable BICs are unique in that we can use weak perturbations to change the confinement dimension of a wave between one, two, and three, making a device which functions simultaneously as a quantum well, a quantum wire, and a quantum dot. Additionally, I showed that weak perturbations can allow us to store a wave indefinitely, and then release it in a direction of choice [illustrated in the static plots]. These two applications may represent another advantage of BICs over traditional methods of localizing waves.