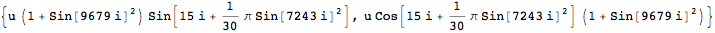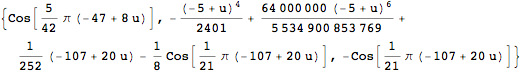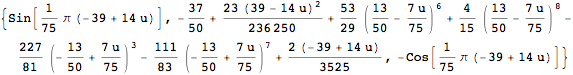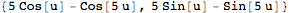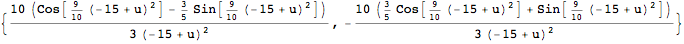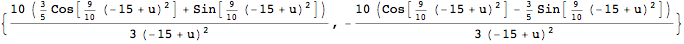Inventory
|
Acceptance Letter to MIT
 |
Anger Management Book
 |
Architect’s Compass
 |
Bargaining Chips
 |
Broken Twig
 |
Burnt Sulfur Lugnut
 |
Cardiac Devices
 |
Denial of Service Attack Plan
 |
|
Depression-Era Clothing
 |
Domestic Avocado
 |
Faded Sofa
 |
Fancy Pocketwatch
 |
Harlequin Doll
 |
Iron Shovels
 |
Leviticus Single
 |
Lil’ String Bikini
 |
|
Little Statue of Liberty
 |
Lottery Numbers
 |
Madman’s Jackal Mask
 |
Mint-Flavored Salami
 |
Mississippi Collectible
 |
Nebular Gloves
 |
Neural Blade
 |
Officer’s Truncheons
 |
|
Old Deuteronomy Sheet Music
 |
Polyatomic Robot
 |
Red Pinafore
 |
Sega Genesis
 |
Severe Beret
 |
Shield of Judgment
 |
Sienna Notebook
 |
Soldierly Parasol
 |
|
Sparkling Necklace
 |
Super-Accurate Tri-Square
 |
Tacky Jeweled Helm
 |
Tamil Liqueur
 |
Ultima III: Exodus
 |
Ultrasonic Boots
 |
Unsafe Mtorolite
 |
Worn Loop of Gold
 |
| Printable Inventory | |||||||