PART 5: Minkowski's words are in boldface.

The electrodynamics of moving bodies ought to have something to do with relativity!
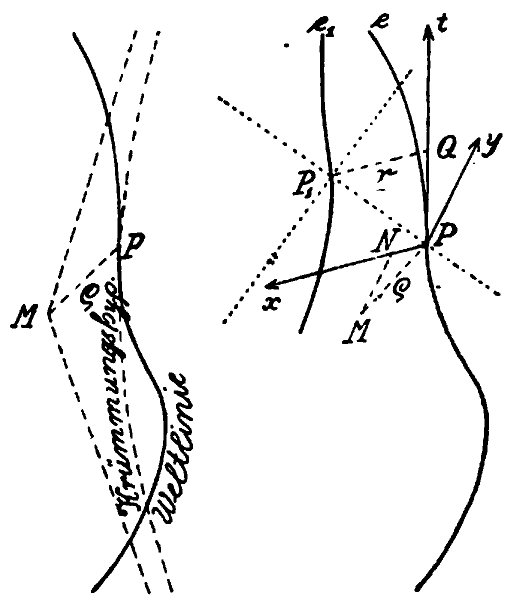
"Let us consider the world-line of such a point-electron with charge e and introduce the proper time τ from any initial point. To obtain the field determined by the electron at any world-point P1 we construct the past-cone P1 (see figure, right). This meets the infinite world-line of the electron at a single point P because its [i.e. the world-line's] directions are everywhere those of a time vector."
To reiterate, the electron is instantaneously at P. The electric field from the electron travels at the speed of light along a light-cone, and hits the other particle's world-line at P1.
"We construct [PQ]the tangent at P to the world-line and through P1 the normal P 1Q to this tangent. Let the scalar [magnitude] of P1Q be r. Then, according to the definition of a past cone we must take the scalar value of PQ as r/c.
"Now the vector in the direction PQ of length e/r represents in its components along the x-, y-, z-axes the vector potential multiplied by c, and in the component along the t-axis the scalar potential of the field produced by e for the world-point P1 . This is the basis of the fundamental laws established by A. Liénard and E. Wiechert, [A. Liénard, "Champ électrique et magnétique produit par une charge concentrée en un point et animée d'un mouvement quelconque," in L'éclairage électrique, Vol. XVI, 1898, pp. 5, 53, 106; E. Wiechert, "Elektrodynamische Elementargesetze" in Archives néerlandaises des sciences exactes et naturelles (2), Vol. V, 1900, p. 549.]"
A clear (but vector-calculus based) discussion of the electric potential from a moving charge can be found here, but the details are not necessary. The point which the reader should take away from this paragraph is that the four fairly-complicated equations describing the four components of the electromagnetic potential can be viewed as a single equation in four dimensional space.
Once the fundamental Minkowski insight of four-dimensionality is gained, many things in physics become obvious. Electric potential is one of numerous physically-important quantities which come in groups of 3 + 1. For example, there is voltage, which is just a number (so many volts), and there is also a closely-related vector quantity, the vector potential, which has x, y, and z components. Similarly, there is energy -- just a number, so many joules -- and there is momentum, a vector with three components. And so on, through the whole of physics. All of these seem reminiscent of time (one dimension) and space (three dimensions). If time and space are directions in a single four-dimensional continuum, each of these sets of 3 + 1 physical quantities might be a four-dimensional vector, with the t-component being the anomalous "just a number" member of the quartet.
"In the description of the field itself produced by the electron it is clearly seen that the separation of the field into electric and magnetic forces is a relative one depending on the time axis of reference. Both forces can be described together most luminously after the analogy, however imperfect, of a force screw in mechanics."
To describe how the electromagnetic field fits into the four-dimensional world-view would take too long, but the general idea is that the three components of the electric field and the three components of the magnetic field are the six components of a special object (called an antisymmetric tensor, a 2-form, or a bivector depending on one's tribal affiliations) which arises naturally in four dimensions. One might think of this as somehow related to the six planes which can be constructed in four-dimensional space: xy, yz, zx, xt, yt, zt.
In the next paragraph, which the non-physicist may wish to skip, Minkowski gives the four-dimensional formula for the force exerted by one charge on the other; the point, as before, is that this expression, complicated as it may look, is a vast simplification when compared to the four separate expressions in the standard literature.
The reader may wonder what the fourth component of force may be. If we recall that force is the rate of change of momentum per unit (proper) time, and that energy is the time-component of momentum, we can see that the time-component of force must be (with appropriate factors of c to get the units right) the rate of change of energy per unit (proper) time, that is, the (proper) power.

"I shall now describe the ponderomotive effect of one
point-charge moving at will on another point-charge moving at will. Let
us take the world-line of the second point-electron of charge
e1,
passing through the world-point P . Let us determine P, Q, r as
before, then (see figure, right) construct the center M of the hyperbola of
curvature at P, and finally the normal MN from M to a straight
line through P parallel to QP1. Let us next determine with P as
origin a system of reference with the t-axis in the direction of PQ,
the x-axis in the direction of QP1,
the y-axis in the direction of MN,
so that finally the direction of the z-axis is determined as normal
to the t-, x-, y-axes. Let the acceleration vector at P be
![]() and the velocity-vector at P1 be
and the velocity-vector at P1 be
 .
Now the action of
the moving force-vector of the first electron e moving at will on the
second electron e1 moving at will at P1
is formulated thus:
.
Now the action of
the moving force-vector of the first electron e moving at will on the
second electron e1 moving at will at P1
is formulated thus:

in which the three relations between the components
 of the vector
of the vector
 are:
are:
 and lastly, this vector
and lastly, this vector
 is normal to the velocity-vector at P1
and through this circumstance alone is dependent on the latter
velocity-vector.
is normal to the velocity-vector at P1
and through this circumstance alone is dependent on the latter
velocity-vector.
"If we compare this statement with the previous formulation of the same fundamental law of the ponderomotive effect of moving point-charges on each other, [found in K. Schwarzschild, Nachrichten der k. Gesellschaft der Wissenschaften zu Göttingen (mathematisch-physikalische Klasse), 1903. p. 132, or H. A. Lorentz, Enzyklopädie der mathematischen Wissenschaften, Vol. V, Art. 14, p. 199] we cannot but grant that the relations here coming under observation do not manifest their intrinsic character of utter simplicity except in four dimensions, but throw a very complicated projection upon a tri-dimensional space preimposed upon them."
The "character of utter simplicity" only "manifest ... in four dimensions" is what makes relativity among the most beautiful of all scientific theories. Minkowski is the first relativist to perceive the wonderful æsthetic quality of the new physics.
"In mechanics reformed according to the world-postulate the disagreements which have caused friction between the Newtonian mechanics and modern electrodynamics disappear of their own accord. I shall touch upon the relation of the Newtonian law of attraction to this postulate."
This section of Minkowski's talk necessarily points to the future: the relativistic theory of gravity will only be developed by Einstein over the coming decade, and a unified theory of gravity and electromagnetism (at least one acceptable to the majority of physicists) will famously resist discovery even in the Twenty-first Century.
"I shall assume that when two point-masses m and m1 describe their world-lines, a moving force-vector acts from m on m1 just as in the above expression in the case of electrons, except that now mm1 is to be substituted for -ee1."
Newton's law of gravity and Coulomb's law of electrostatic attraction are closely analogous. It is natural for Minkowski to begin with this analogy.
"We shall now consider especially the particular case where the acceleration-vector of m is constantly zero, in which case we can so introduce t that m is conceived of as at rest, and the motion of m1 depends only on the moving force-vector proceeding from m. If we modify this vector first by the factor

which, up to quantities of the order 1/c² is equal to 1, then it follows that for positions x1, y1, z1 of m1and their corresponding time-positions, Kepler's laws would again obtain, except that in place of the times t1 the proper time τ1 of m would be substituted."
The full argument is found in H. Minkowski, Ges. Abhandlungen, II, p. 403.
"On the basis of this simple observation we can see that the proposed law of attraction in conjunction with the new mechanics would be no less suitable for explaining astronomical observations than Newton's law of attraction in conjunction with the Newtonian mechanics."
In fact, gravity will turn out to be a bit more complex than this.
"The fundamental equations for electromagnetic processes in ponderable bodies are likewise in complete harmony with the world-postulate. Even the derivation of these equations, as taught by Lorentz on the basis of conceptions of the electron theory, need not for this end by any means be abandoned, as I shall show elsewhere. [H. Minkowski, Ges. Abhandlungen, II, p. 405.]"
We come at last to the end of this historic talk:
"The universal validity of the world-postulate is, I should believe, the true core of an electromagnetic world-picture; first discovered by Lorentz, then further developed by Einstein, it is now clearly discernible. In the future development of its mathematical consequences enough indications will be found for experimental verification of the postulate to reconcile by the idea of a pre-established harmony between pure mathematics and physics even those to whom a surrender of old accustomed view-points is uncongenial or painful."
--- HERMANN MINKOWSKI.
The audience in Cologne applauds.
In the epilogue to this edition of Raum und Zeit, we will present a brief synopsis of special relativity from a more modern but still Minkowskian perspective.
TIME AND SPACE, by Hermann Minkowski