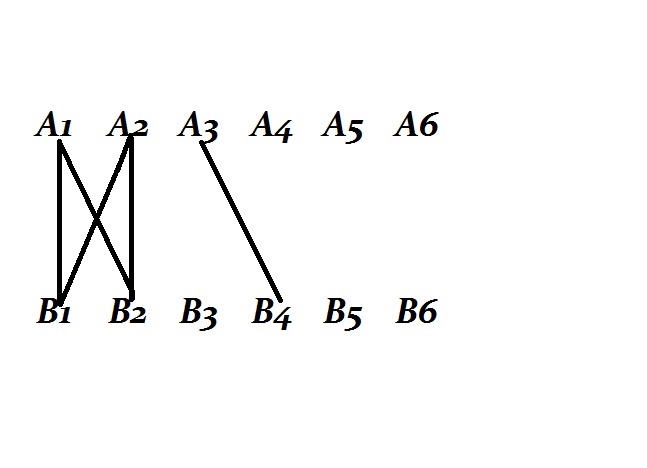
An input-output network.
2013 June 8
PART 4: Poincaré's words are in boldface.

Why have all these spaces three dimensions ? Go back to the "table of distribution" of which we have spoken. We have on the one side the list of the different possible dangers; designate them by A1, A2, etc. ; and on the other side, the list of the different remedies which I shall call in the same way B1, B2, etc. We have then connections between the contact studs or push buttons of the first list and those of the second, so that when, for instance, the announcer of danger A3 functions, it will put or may put in action the relay corresponding to the parry B4.
As I have spoken above of centripetal or centrifugal wires, I fear lest some one see in all this, not a simple comparison, but a description of the nervous system. Such is not my thought for several reasons: first, I should not permit myself to put forth an opinion on the structure of the nervous system which I do not know, while those who have studied it speak only circumspectly; again, because, despite my incompetence, I well know this scheme would be too simplistic ; and, finally, because on my list of parries, some would figure very complex, which might even, in the case of extended space, as we have seen above, consist of many steps followed by a movement of the arm. It is not a question then of physical connection between two real conductors, but of psychologic association between two series of sensations.
If A1 and A2 for instance are both associated with the parry B1, and if A1 is likewise associated with the parry B2, it will generally happen that A2 and B2 will also themselves be associated.
If this fundamental law were not generally true, there would exist only an immense confusion and there would be nothing resembling a conception of space or a geometry. How in fact have we defined a point of space? We have done it in two ways: it is on the one hand the aggregate of announcers A in connection with the same parry B; it is on the other hand the aggregate of parries B in connection with the same announcer A. If our law was not true, we should say A1 and A2 correspond to the same point since they are both in connection with B1; but we should likewise say they do not correspond to the same point, since A1 would be in connection with B2 and the same would not be true of A2. This would be a contradiction.
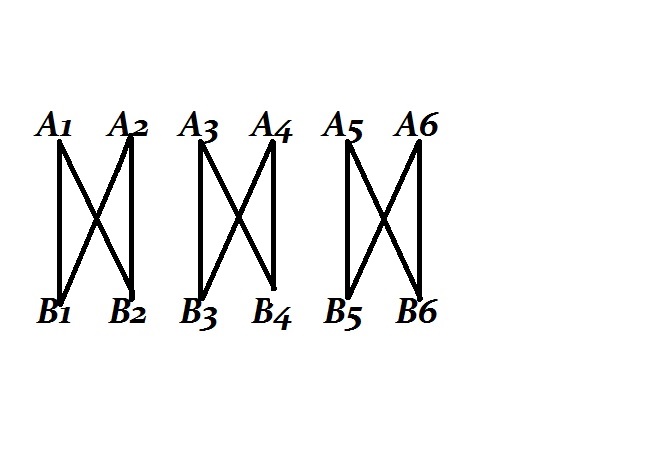
But, from another side, if the law were rigorously and always true, space would be very different from what it is. We should have categories strongly contrasted between which would be portioned out on the one hand the announcers A, on the other hand the parries B; these categories would be excessively numerous, but they would be entirely separated one from another. Space would be composed of points very numerous, but discrete; it would be discontinuous. There would be no reason for ranging these points in one order rather than another, nor consequently for attributing to space three dimensions.
But it is not so ; permit me to resume for a moment the language of those who know geometry ; this is quite proper since this is the language best understood by those I wish to make understand me.
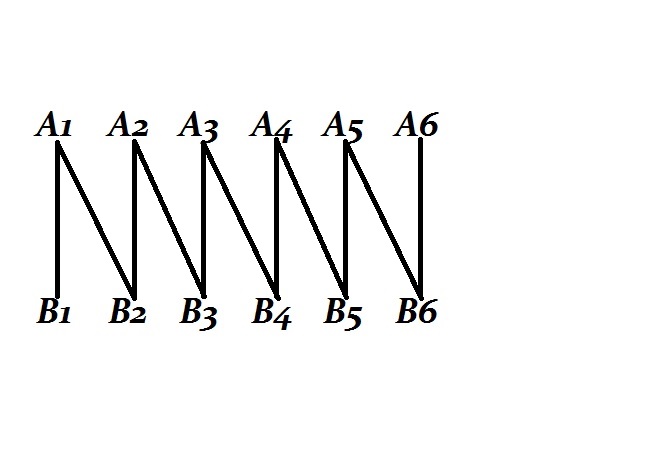
When I desire to parry the stroke, I seek to reach the point from which the blow comes, but it suffices that I approach quite near. Then the parry B2 may answer for A1 and for A2, if the point which corresponds to B2 is sufficiently near both to that corresponding to A1 and to that corresponding to A2.
But it may happen that the point corresponding to another parry B1 may be sufficiently near the point corresponding to A1 and not sufficiently near the point corresponding to A2 ; so that the parry B1 may answer for A1 without answering for A2.
[In the printed versions B1 and B2 above are switched; this seems to be a typographical error, and I have corrected the notation to agree with the rest of the essay. -- Editor]
For one who is not acquainted with geometry, this translates itself simply by a derogation of the law stated above. And then things will happen thus: Two parries B1 and B2 will be associated with the same warning A1 and with a large number of warnings which we shall range in the same category as A1 and which we shall make correspond to the same point of space.
But we may find warnings A2 which will be associated with B2 without being associated with B1, and which in compensation will be associated with B3, which B3 was not associated with A1, and so forth, so that we may write the series
where each term is associated with the following and the preceding, but not with the terms several places away. Needless to add that each of the terms of these series is not isolated but forms part of a very numerous category of other warnings or of other parries having the same connections, and which may be regarded as belonging to the same point of space.
The fundamental law, though admitting of exceptions, remains therefore almost always true. Only, in consequence of these exceptions, these categories, in place of being entirely separated, encroach partially one upon another and mutually penetrate in a certain measure, so that space becomes continuous.
On the other hand, the order in which these categories are to be ranged is no longer arbitrary, and if we refer to the preceding series we see it is necessary to put B2 between A1 and A2 and consequently between B1 and B3, and that we could not for instance put it between B3 and B4 .
There is therefore an order, corresponding to the points of space, in which we naturally arrange our categories, and experience teaches us that this order presents itself under the form of a table of triple entry, and this is why space has three dimensions.

EDITOR'S NOTES:
Although Poincaré begins and ends this section with comments on tridimensionality, he never really addresses the question of why space should have this property: that discussion would have to wait for Ehrenfest a few years later. What Poincaré does consider is why space seems to be continuous. His answer takes us from biology to computer science.
According to Poincaré geometrical expressions such as distance are abstractions from algorithms coupling "warnings of threats" (stimuli) to "parries" (responses, in the form of complex motions). If, after performing one sequences of movements with my right hand and another with my left, I find that my two hands are together, I say that the two sequences correspond to the same point in space, and this is what the term "point in space" means.
Galileo's Simplicio would snort: "Well, of course they're at the same point in space; that's why they bumped into each other. Space is out there, and your hands move around in it!" To answer this objection, Poincaré has to show that stimulus-response couplings can reproduce all the properties of space, such as its continuity.
The implication of his success in this should be disturbing, but probably isn't -- Twenty-first Century people take the conclusion for granted. Consider a video game, perhaps one set in Paris in 1906. The object of the game is to get one's avatar from Poincaré's house to the Place de Panthéon, collecting one-franc coins scattered along the route. Assuming the game is well designed, the player sees the world through the avatar's eyes. Distant buildings appear small, then become larger as one approaches them. An appropriate motion of the joystick enables the avatar to turn corners, to board a passing omnibus, to pick up and examine the one-franc coins. If the game is a very primitive one, say from the 1980s, there may be a jerky, stroboscopic quality to the experience, but if it is modern all these movements will seem smooth and continuous. And yet -- nothing is really moving except for electrons in the IC chip and light from the screen. There are no corners to round, no omnibuses to board, no coins to collect, no neighbourhoods to explore, and no avatars to do the exploring. There are just algorithms which require that, if such-and-such pixels are currently illuminated and the joystick transmits such-and-such a signal, then a particular new pattern of pixels will replace the old one.
In Poincaré's view, the daily reality we experience is just like the virtual reality of the game. Space is not "out there" any more than 1906 Paris is in one's monitor, but there are rules linking inputs to outputs which create that illusion. This is another reason why Poincaré is wise to insist that his "centrifugal and centripetal wires" are not necessarily the nervous system. Even if the nervous system's operation could be placed in one-to-one correspondence with the input-output coupling-network, it could be (as we would say now) merely emulating the actual hardware on which the program is running -- an unsettling Thirteenth Floor version of the Church-Turing thesis!

THE RELATIVITY OF SPACE, by Henri Poincaré