Logic diagrams have a long history, told so well by Martin Gardner [Logic Machines and Diagrams, New York: McGraw-Hill, 1958] that it would be pointless to repeat it here. Of all the methods devised in the centuries since Ramon Llull's, only one seems to have worked its way into the general consciousness. This, of course, is the so-called Venn diagram (not truly Venn's; he himself attributed it to Euler, and it probably goes back to an earlier era yet).

The Venn diagram's success, of course, lies in its all but self-explanatory nature. Even when there are many classes to compare, the Venn diagram is sometimes obvious -- at least when quite a few of the classes lie in a nested hierarchy.
[Wikipedia]
Slightly less well-ordered systems, though, can be a bit of a mess:

Amino acids, by Klaus Hoffmeier, after W. R. Taylor [J. Theor. Biol. 119, 205 (1986)].
Logicians of the Long Nineteenth Century -- Venn's century -- were well aware of this defect, and produced many other kinds of diagrams in the hope of fixing it. Here is one of the best, invented by a rather obscure American professor of philosophy and psychology. It seems never to have been widely known, which is typical of such things: Babbage and Lovelace were far from the only neglected pioneers of computer science.

Amherst College, Amherst, Mass., 1906. [Library of Congress]
by William J. Newlin
[Journal of Philosophy 3, 239 (1906).] Newlin's words are in bold.
The diagram is a non-essential in logic; but the increased tendency on the part of comparatively recent writers towards its use would seem to indicate that it has a decidedly practical illustrative and educational value. Unfortunately all diagrams which have as yet been proposed labor under some more or less serious disadvantage. It is the purpose of this paper to present a diagram which, it is hoped, will prove to be a step towards the desired ideal.
The demands which a satisfactory diagram must meet are few, but vital:
First, there must be a complete symmetrical one-one correspondence between the elements of the diagram, whatever they may be, and the elements of the given logical universe. These latter elements consist of all of the possible combinations of the classes considered, or of their symbolic representatives. This condition demands that the diagrammatic elements, like the symbolic ones, be mutually exclusive and collectively exhaustive. If the diagram is to be of practical utility, it must, by the very nature of its construction, secure complete one-one correspondence automatically for any number of classes; thus relieving the user of all responsibility as to whether every symbolic subclass has its graphical representative in his diagram or not : not a simple matter when it is considered that successive addition of classes involves successive doubling of the number of subclasses.
Secondly, if the diagram is to be practically valuable, it must be simple in construction and appearance, free from any possible source of confusion, readily adaptable to any desired modification of conditions and, in general, its manipulation must be easy, quick and reliable.
Lastly, as the number of classes considered increases, the diagram must keep pace with the increasing symbolic notation with perfect correspondence and simplicity; in one word, it must be "simply- extensible."
The shortcomings of the usual diagrams are familiar to all. The Eulerian circles, at their best, are limited to the case of three-class representation, for which, it is true, they serve admirably. The four-ellipse system for four-class representation, as proposed by Mr. Venn, is confusing at first. A five-ellipse system fails to represent five-class combinations; and Mr. Venn's modification creates more confusion than ever. These difficulties were recognized by Mr. Venn, for he questions the utility of such diagrams for extension beyond the five-class case.
The diagram of Dr. H. Marquand [Philosophical Magazine V 12, 266 (1881)] comes nearest to satisfying all the conditions ; there is no question as to its extensibility and its perfect correspondence ; but it has the disadvantage that the elements of a single class are in discrete groups, even in the simplest possible cases, and this involves unnecessary complexity.
In the design of the following diagram the attempt has been made to utilize the bisection principle and class-group units in a multiple self-representative series so that the result may have the good features of each method without its faults.
The unit chosen is the four-class diagram, and the geometrical form of it is that of the square, since this figure lends itself most readily to unit combinations of the kind desired; and it has been so subdivided as to be adapted to class representation up to and including seven classes ; so that the unit itself will serve the purpose for all ordinary cases. At the same time its manipulation is not so complex as to make it in any degree confusing to the student, and its colligation for extension is of the simplest possible kind.
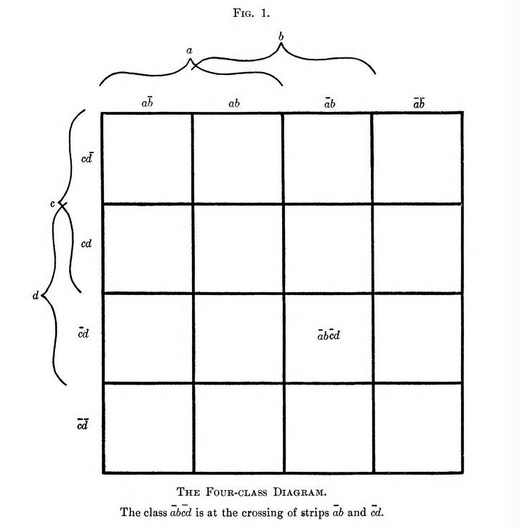
Let the logical universe be represented by a square (hereinafter referred to as the "primary" square), divided by vertical lines into four vertical strips, and by horizontal lines into four horizontal strips.
Let class a be represented by the first and second vertical strips, counting from left to right, taken together ; and class b by the second and third, taken together.
Let class c be represented by the first and second horizontal strips, counting down, taken together; and class d by the second and third, taken together.
Then the individual vertical strips will represent in order a b̄, ab, ā b, ā b̄; and the horizontal strips will represent c d̄, c d, c̄ d, c̄ d̄ [where ā means "not a", &c.]
Any combination of these pairs of terms may be found at once with great ease, as the particular "secondary" square representing the logical product under consideration will be at the intersection of the two strips which represent these term-pairs.
This figure is easily constructed, and offers no possible chance for confusion; and the symmetry of the indicative notation makes it easily remembered, and simple in use.
This figure may be adapted to three-class representation by making c a zero class, i. e., erase the upper half of the diagram : and to two-class representation by making d also a zero class, leaving only the bottom row.
To represent the relations of five classes, construct the diagram as before for any four of the five classes. Then in addition add to the figure all possible diagonals in one direction : (diagonal bisectors have been introduced in preference to horizontal or vertical ones, to avoid confusion with the existing strips). Consider these diagonals as sides of diagonal strips, and let one of the two sets of alternate diagonal strips represent the fifth class.
Each secondary square is now subdivided into two triangles, each of which will have the same class-product of a, b, c, d as before; but one of them has this product combined with e, and the other, this same product combined with ē.
The process of locating any of the thirty-two possible subclasses is identically the same as for a four-class product, augmented merely by the choice of two specific triangles to meet a fifth-class demand.
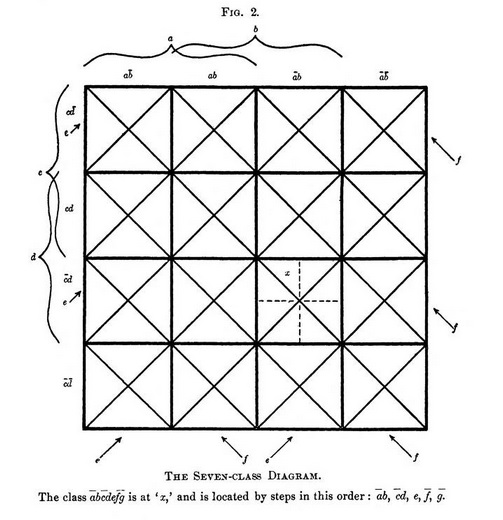
For six-class representation, add to the primary square both sets of diagonals, and let one of the two sets of alternate diagonal strips represent the fifth class, and one of the two sets of opposite-diagonal strips represent the sixth class.
Each secondary square is now subdivided into four triangles. Classes a, b, c, d determine the secondary square as before; classes e, f determine which of the four specific triangles is to be taken; and the proper subdivision is thus located easily, quickly and with certainty.
A further subdivision of the secondary square by lines through its center parallel to its sides (shown dotted in a typical square in Fig. 2), together with the convention that of the subdivisions of the four triangles the right or upper half, as the case may be, shall represent g, and the other half ḡ, renders possible the clear representation of the 128 subclasses of the seven classes a . . . g; and the tracing of any given class-product to the proper secondary square, proper triangle and proper half of the triangle is a simple, short and certain process.
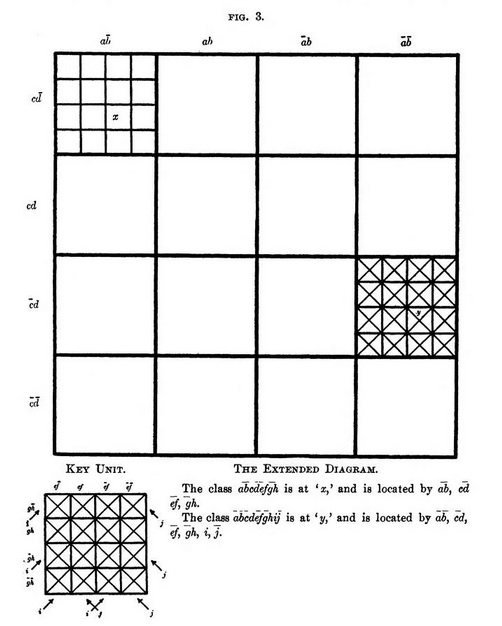
To represent more than seven classes, replace each of the secondary squares in the fundamental four-class diagram by a four-class diagram as a unit. The resulting figure contains all possible eight-class combinations, each of which may be located in two similar steps; one to locate the secondary square, now itself of primary form, and one to locate its proper secondary square. These latter squares will be referred to as "tertiary."
Modifications of the secondary square unit as already described for five, six or seven classes will adapt the entire figure to representation of nine, ten or eleven classes; after which, replacing the tertiary square by the four-class unit, and its successive modifications, will extend the diagram by a process which is clearly recurrent, and indefinitely continuous.
It will be found a practical advantage for very complex cases to use, for each four-class set, a typical unit as a key, on which its particular four-class notation is marked, rather than to confuse the primary square by a superabundance of class terms; and also on account of the fact that by the use of such a key the actual construction of the complete diagram need be carried out in extreme detail in those portions only to which the conditions of the problem under discussion apply.
From the method of its construction it is evident that this diagrammatic scheme furnishes perfect correspondence for any number of classes. The four-class unit, with its modifications, is simple; and on account of the recurrent character of the extension process, with the use of key units, the manipulation of the diagram never can become more complex than in the seven-class case.
Wm. J. Newlin.
Amherst College.
How well does Newlin's method work? Here is the classification of amino acids, along with the Venn diagram we saw earlier. (To save space, I have used "X" and "Z" for the two "C" amino-acids.)

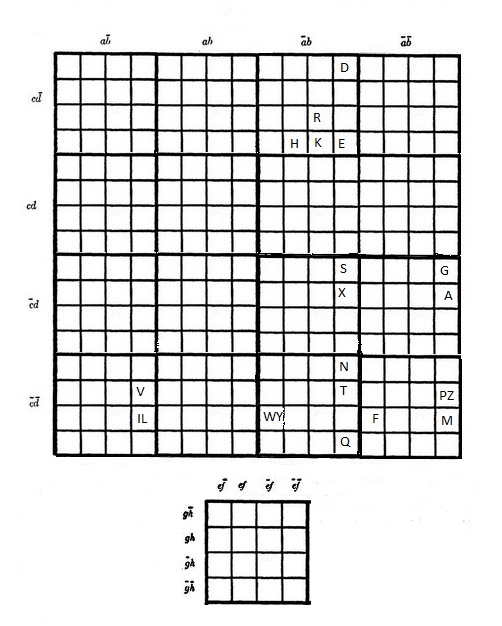
a = aliphatic;
b = polar;
c = charged;
d = tiny;
e = aromatic;
f = positive;
g = small;
h = hydrophobic;
Whether the Newlin diagram is superior to the Venn diagram is perhaps a matter of taste. In the process of drawing the figure, I made two observations.
The first is that the original Venn diagram was certainly hard to read: try following the border of the "hydrophobic" class, for example! This is a defect of the particular drawing, but it would be hard to avoid under any circumstances.
The second is that the Newlin diagram would look quite different if I had assigned the variables a, b, ... differently. I made the assignments on the basis of the English words they represented (a for "aliphatic", for example). Perhaps there is some natural choice, in which the fact that "tiny" is a subset of "small", for instance, would be reflected in the naming convention. It might be interesting, though tedious, to generate all possible Newlin diagrams of the amino acids, that is with every possible naming convention, and see whether any over all pattern emerges.
This is a form of the "arbitrary catalogue" problem in taxonomy. Suppose we wish to classify plants as botanical fruit, culinary vegetables, neither, or both (as in one of the earlier Venn diagrams). A simple numerical scheme might represent the "neither" option as "zero" (00 in binary) and the "both" option as "three" (11 in binary). But does "one" (01) mean "a vegetable which is not a fruit" or "a fruit which is not a vegetable"? The answer is clearly arbitrary, subject only to the constraint that "two" (10) must mean the opposite of whichever we chose. And yet the numbers "one" and "two" have different mathematical properties! A "natural" (or perhaps one should say a "divine") scheme would be one in which there was some isomorphism between, say, an apple and the number "two" which does not exist between a carrot and the number "two".
The likelihood of such an isomorphism would seem intuitively to decrease from an already low start as the number of classes increases. We could classify an amino acid by an eight-digit binary number, but it is difficult to believe that the arithmetical properties of the number would of themselves teach us much biochemistry.
Is this true? Looking at the clusters in the Newlin diagram of a complex system, one sees (some) apparent order. How much of this order is due to the arbitrary assignment of variables by the modeller, and how much to the system itself?