Henry Ernest Dudeney, the son and grandson of school-masters, had only an elementary education, and spent his life working as a clerk and journalist ; nevertheless, he was arguably one of the most successful mathematics teachers of his era. Dudeney was a leading figure in the great recreational-mathematics boom of the late Nineteenth Century, writing mathematical-puzzle columns in The Strand Magazine and other publications. His goals always went beyond entertainment : in a famous 1917 essay he declared that the history of puzzles is "nothing short of the actual story of the beginnings and development of exact thinking in man."
In fact, many of Dudeney's puzzles had extraordinary mathematical depth, and some continue to inspire serious research today. (This can sometimes produce amusing results ; earlier this year an e-print by Ed Wynn appeared on arXiv with the title Exhaustive generation of "Mrs Perkins's quilt" square dissections for low orders.) Dudeney also anticipated very recent thinking, unfashionable for much of the Twentieth Century, about the value of experiment in mathematics, remarking: "Even those puzzles that we have no way of attacking except by haphazard attempts can be brought under a method of what is called 'glorified trial' -- a system of shortening our labours by avoiding or eliminating what our reason tells us is useless. It is, in fact, not easy to say sometimes where the 'empirical' begins and where it ends."
Dudeney owed much of his success to his literary style, always framing his puzzles as stories ; one of his most famous collections was entitled The Canterbury Puzzles. Although neither a Chaucer nor a Lewis Carroll, he remains readable today, more than can be said for many a mathematician. As he himself put it in the preface to Amusements in Mathematics: "It is possible that some few exceedingly sober-minded mathematicians, who are impatient of any terminology in their favourite science but the academic, and who object to the elusive x and y appearing under any other names, will have wished that various problems had been presented in a less popular dress and introduced with a less flippant phraseology. I can only refer them to the first word of my title and remind them that we are primarily out to be amused -- not, it is true, without some hope of picking up morsels of knowledge by the way. If the manner is light, I can only say, in the words of Touchstone, that it is an ill-favoured thing, sir, but my own; a poor humour of mine, sir."
Holiday greetings from The Net Advance of Physics!

THE SQUIRE'S CHRISTMAS PUZZLE PARTY
by Henry Ernest Dudeney
from The Canterbury Puzzles, and Other Curious Problems, second edition,
[London: Thomas Nelson, 1919].
Dudeney's words are in bold.
A fine specimen of the old English country gentleman was Squire Davidge, of Stoke Courcy Hall, in Somerset. When the last century was yet in its youth, there were few men in the west country more widely known and more generally respected and beloved than he. A born sportsman, his fame extended to Exmoor itself, where his daring and splendid riding in pursuit of the red deer had excited the admiration and envy of innumerable younger huntsmen. But it was in his own parish, and particularly in his own home, that his genial hospitality, generosity, and rare jovial humour made him the idol of his friends --- and even of his relations, which sometimes means a good deal.
At Christmas it was always an open house at Stoke Courcy Hall, for if there was one thing more than another upon which Squire Davidge had very pronounced views, it was on the question of keeping up in a royal fashion the great festival of Yule-tide. "Hark ye, my lads," he would say to his sons : "our country will begin to fall on evil days if ever we grow indifferent to the claims of those Christmas festivities that have helped to win us the proud name of Merrie England." Therefore, when I say that Christmas at Stoke Courcy was kept up in the good old happy, rollicking, festive style that our grandfathers and great-grandfathers so dearly loved, it will be unnecessary for me to attempt a description. We have a faithful picture of these merry scenes in the Bracebridge Hall of Washington Irving. I must confine myself in this sketch to one special feature in the Squire's round of jollification during the season of peace and good will.
He took a curious and intelligent interest in puzzles of every kind, and there was always one night devoted to what was known as "Squire Davidge's Puzzle Party." Every guest was expected to come armed with some riddle or puzzle for the bewilderment and possible delectation of the company. The old gentleman always presented a new watch to the guest who was most successful in his answers. It is a pity that all the puzzles were not preserved ; but I propose to present to my readers a few selected from a number that have passed down to a surviving member of the family, who has kindly allowed me to use them on this occasion. There are some very easy ones, a few that are moderately difficult, and one hard brain-racker, so all should be able to find something to their taste.
The little record is written in the neat angular hand of a young lady of that day, and the puzzles, the conditions of which I think it best to give mainly in my own words for the sake of greater clearness, appear to have been all propounded on one occasion.
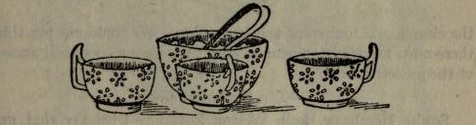
THE THREE TEACUPS
One young lady --- of whom our fair historian records with delightful inconsequence : "This Miss Charity Lockyer has since been married to a curate from Taunton Vale " --- placed three empty teacups on a table, and challenged anybody to put ten lumps of sugar in them so that there would be an odd number of lumps in every cup. "One young man, who has been to Oxford University, and is studying the law, declared with some heat that, beyond a doubt, there was no possible way of doing it, and he offered to give proof of the fact to the company." It must have been interesting to see his face when he was shown Miss Charity's correct answer.

THE ELEVEN PENNIES
A guest asked some one to favour him with eleven pennies, and he passed the coins to the company, as depicted in our illustration. The writer says : "He then requested us to remove five coins from the eleven, add four coins and leave nine. We could not but think there must needs be ten pennies left. We were a good deal amused at the answer hereof."

THE CHRISTMAS GEESE
Squire Hembrow, from Weston Zoyland --- wherever that may be --- proposed the following little arithmetical puzzle, from which it is probable that several somewhat similar modem ones have been derived : Farmer Rouse sent his man to market with a flock of geese, telling him that he might sell all or any of them, as he considered best, for he was sure the man knew how to make a good bargain. This is the report that Jabez made, though I have taken it out of the old Somerset dialect, which might puzzle some readers in a way not desired.
"Well, first of all I sold Mr. Jasper Tyler half of the flock and half a goose over ; then I sold Farmer Avent a third of what remained and a third of a goose over ; then I sold Widow Foster a quarter of what remained and three-quarters of a goose over ; and as I was coming home, whom should I meet but Ned Collier : so we had a mug of cider together at the Barley Mow, where I sold him exactly a fifth of what I had left, and gave him a fifth of a goose over for the missus. These nineteen that I have brought back I couldn't get rid of at any price."
Now, how many geese did Farmer Rouse send to market? My humane readers may be relieved to know that no goose was divided or put to any inconvenience whatever by the sales.

THE CHALKED NUMBERS
"We laughed greatly at a pretty jest on the part of Major Trenchard, a merry friend of the Squire's. With a piece of chalk he marked a different number on the backs of eight lads who were at the party." Then, it seems, he divided them in two groups, as shown in the illustration, 1, 2, 3, 4 being on one side, and 5, 7, 8, 9 on the other. It will be seen that the numbers of the left-hand group add up to 10, while the numbers in the other group add up to 29. The Major's puzzle was to rearrange the eight boys in two new groups, so that the four numbers in each group should add up alike. The Squire's niece asked if the 5 should not be a 6 ; but the Major explained that the numbers were quite correct if properly regarded,

TASTING THE PLUM PUDDINGS
"Everybody, as I suppose, knows well that the number of different Christmas plum puddings that you taste will bring you the same number of lucky days in the new year. One of the guests (and his name has escaped my memory) brought with him a sheet of paper on which were drawn sixty-four puddings, and he said the puzzle was an allegory of a sort, and he intended to show how we might manage our pudding-tasting with as much dispatch as possible."
I fail to fully understand this fanciful and rather overstrained view of the puzzle. But it would appear that the puddings were arranged regularly, as I have shown them in the illustration, and that to strike out a pudding was to indicate that it had been duly tasted. You have simply to put the point of your pencil on the pudding in the top corner, bearing a sprig of holly, and strike out all the sixty-four puddings through their centres in twenty-one straight strokes. You can go up or down or horizontally, but not diagonally or obliquely; and you must never strike out a pudding twice, as that would imply a second and unnecessary tasting of those indigestible dainties. But the peculiar part of the thing is that you are required to taste the pudding that is seen steaming hot at the end of your tenth stroke, and to taste the one decked with holly in the bottom row the very last of all.

UNDER THE MISTLETOE BOUGH
"At the party was a widower who has but lately come into these parts," says the record; "and, to be sure, he was an exceedingly melancholy man, for he did sit away from the company during the most part of the evening. We afterwards heard that he had been keeping a secret account of all the kisses that were given and received under the mistletoe bough. Truly, I would not have suffered any one to kiss me in that manner had I known that so unfair a watch was being kept. Other maids beside were in a like way shocked, as Betty Marchant has since told me." But it seems that the melancholy widower was merely collecting material for the following little osculatory problem.
The company consisted of the Squire and his wife and six other married couples, one widower and three widows, twelve bachelors and boys, and ten maidens and little girls. Now, everybody was found to have kissed everybody else, with the following exceptions and additions : No male, of course, kissed a male. No married man kissed a married woman, except his own wife. All the bachelors and boys kissed all the maidens and girls twice. The widower did not kiss anybody, and the widows did not kiss each other. The puzzle was to ascertain just how many kisses had been thus given under the mistletoe bough, assuming, as it is charitable to do, that every kiss was returned -- the double act being counted as one kiss.
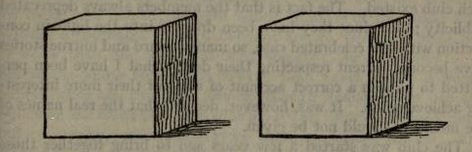
THE SILVER CUBES
The last extract that I will give is one that will, I think, interest those readers who may find some of the above puzzles too easy. It is a hard nut, and should only be attempted by those who flatter themselves that they possess strong intellectual teeth.
"Master Herbert Spearing, the son of a widow lady in our parish, proposed a puzzle in arithmetic that looks simple, but nobody present was able to solve it. Of a truth I did not venture to attempt it myself, after the young lawyer from Oxford, who they say is very learned in the mathematics and a great scholar, failed to show us the answer. He did assure us that he believed it could not be done, but I have since been told that it is possible, though, of a certainty, I may not vouch for it.
"Master Herbert brought with him two cubes of solid silver that belonged to his mother. He showed that, as they measured two inches every way, each contained eight cubic inches of silver, and therefore the two contained together sixteen cubic inches. That which he wanted to know was --- Could anybody give him exact dimensions for two cubes that should together contain just seventeen cubic inches of silver?" Of course the cubes may be of different sizes.
The idea of a Christmas Puzzle Party, as devised by the old Squire, seems to have been excellent, and it might well be revived at the present day by people who are fond of puzzles and who have grown tired of Book Teas and similar recent introductions for the amusement of evening parties. Prizes could be awarded to the best solvers of the puzzles propounded by the guests.

Dudeney's solutions to these problems -- some of which, let the solver be aware, are unfair tricks! --- may be found here.