
Photo by Ryan Somma
Visible Sound
2014 April 7

In the previous installment of this series, the opera-singer and voice-teacher Margaret Watts Hughes described a startling acoustical phenomenon that she had discovered in 1885. She would sing into a pipe, the end of which had been covered with an elastic membrane. Fine powder sprinkled on the membrane would then assume complicated shapes reminding her of flowers, serpents, and other improbably biological forms.
Hughes's discovery was taken seriously by the physics community -- up to a point. Visualising the unseen motions of the air was an important research problem -- it would remain so even in the middle of the Twentieth Century, when the late MIT President Charles Vest would devote much of his career to it -- with obvious applications to engineering. If the singer's "eidophone" could help, it was worth investigating (even if the discoverer was a woman). But this was a technical problem : the underlying physics of vibration was well-understood in theory, even if the complexities of vibration piled on vibration in a real system defied analysis. What mattered most to Hughes -- that the shapes were organic, seemingly alive -- struck the Royal Society stalwarts as a flight of feminine fancy.
Nor was this view limited to males. In today's piece, a woman scientist -- or at least a woman science-writer -- presents the Establishment's response to Hughes : sympathetic and encouraging, but also dismissive of her amateurism. The end of the 1800s saw the beginning of the Professional Researcher's domination in science, with all the positive and negative concommittants of that reign.
Sophie Bledsoe Herrick was not a "professional researcher", but she would have been had the possibility existed for a woman of her generation. She informally studied science at the colleges where her father taught, and in middle age attended Johns Hopkins as a biology student. (In between she was married to a scholarly Anglican priest who decided he would rather practise free love at the Oneida Community.) An early convert to Darwinism, Sophie Herrick eventually found her niche as a spokeswoman of the rising scientific Establishment, first as a free-lance science-writer and later as assistant editor of the immensely popular Century Magazine.
Herrick owed at least some of her eventual success to the support of her father, Albert Taylor Bledsoe, who had flourished when eccentricity and amateurism were normal in science. A Kentucky aristocrat who was once an American Anglican priest-mathematician of the Cambridge type, Bledsoe abandoned his career in the Episcopal Church over doctrinal issues. Like many another Nineteenth Century genius, he seemed to live multiple lives : he was a Southern Methodist theologian, a soldier, a writer, a lawyer (at one point practising in Springfield, Illinois, where he competed with Abraham Lincoln), a political theorist, a professor of mathematics, astronomy, and French in various universities ... Regrettably, though, his main legacy was undesirable : his well-written books defending secession and his propaganda magazine The Southern Review played a major role in the former Confederacy's catastrophic intellectual victory over Northern Abolitionist values during Reconstruction (see Terry Barnhart's Albert Taylor Bledsoe: Defender of the Old South and Architect of the Lost Cause [Louisiana State University, 2011] ; Herrick's own biographical note about her father is surprisingly even-handed).
VISIBLE SOUND -- COMMENT
by Sophie B. Herrick
[Century Magazine 42, 40 (1891)]
Hughes's words are in bold.

The article on "Voice-Figures" by Mrs. Watts Hughes gives some very remarkable experiments made by singing into a resonator over which an elastic membrane is stretched. On this membrane some substance (sand, paste, or glycerin) is spread; and when the membrane is set into vibration by the musical note sounding beneath it, the substance above gathers itself together into many wonderful forms. Some slight explanation of the nature of sound, and of certain of its phenomena, may be necessary to make clear to the general reader these experiments of Mrs. Hughes.
A simple conception of a sound-wave may be gained by the use of a device of Professor Tyndall. A small collodion balloon filled with explosive gases is ignited. The report seems to reach the ear as the flash is seen, but there is a fraction of a second between them. The sound has been traveling from the point of explosion to the ear of the observer. It has not been conveyed bodily, as matter shot out from that center, nor borne to it by the movement of the air. If such had been the case, the listener would have been struck by a hurricane progressing at the rate of about seventy-five miles an hour. The wave-motion constituting sound advances, while the medium in which the wave is formed the air only oscillates.
This is true of wave-motion generally. A cord fastened at one end, and held taut by the hand at the other, may be jerked, and a wave will run along it to the fixed end : the wave progressed, while each particle of the cord only made a short excursion, and returned to its old position. A puff of wind, striking a field of standing grain, causes a wave to sweep across the field. Each stalk bends forward, delivers up the impulse it has received to the stalks before it, and returns to its own place.
In the old days when messages were carried by relays of couriers, each courier took his message to a certain point, delivered it up to another messenger, and then returned to his former post ; the second courier, carrying forward the message, in turn delivered it to a third; and so on. The message went on, but each messenger made only a comparatively short excursion. This is a homely, almost, a puerile, illustration, but it serves to show how wave-motion is propagated.
When our little collodion balloon was ignited the gases inside suddenly needed more room, and this they got by bursting the inclosing membrane of the balloon and pressing back the surrounding air in every direction. By this pressure the particles of air were violently crowded together in a spherical shell surrounding the center of explosion. The rebound of the crowded particles threw them farther apart than they were normally, thus crowding back another shell of air-particles outside the first shell, and leaving the first rarefied ; and so the wave-motion advanced. Sound-waves are really only alternate condensations and rarefactions of the air, as water-waves, owing to the slight compressibility and elasticity of the water, show themselves as alternate heaps and hollows.
When a single sonorous impulse or a succession of irregular impulses is imparted to the air, noise is the result. The puff of wind across the wheatfield or the jerk at the taut cord corresponds with what we call noise. When, however, a succession of regular impulses sets the air into sonorous vibration, and these impulses succeed each other with sufficient rapidity to link themselves together in the ear, we have a musical note. Noise is disorder; music is order. Noise jolts the nerves and the brain ; music lulls them by its rhythmic swing.
The pitch of a musical note is determined by the rapidity with which these impulses follow each other. The lowest musical note which the ear can hear, as music, is caused by 16 vibrations per second ; the highest, by 38,000 vibrations per second. The middle C of the piano gives, when struck, 264 vibrations a second. An ordinary seven-octave piano ranges from 33 vibrations per second, three octaves below the middle C, to 4224, four octaves above the middle C.
The simplest form of musical vibration is that generated by a stretched string. It swings to and fro rhythmically when plucked or set in motion by a violin bow, and sets the air into corresponding rhythmic vibrations. It sets such a narrow slice of air in motion, however, that to produce any effect the string has to be reinforced by a body of air in a resonator, as in the violin and the guitar, or by a sounding-board, as in the harp and the piano.
A stretched string like a pendulum makes only a given number of vibrations in a fixed time. It may seem to move more and more slowly, but it is only because the excursions to and fro become shorter and shorter ; the number of vibrations for the same string or other sonorous body are always the same. It must be borne in mind that the length of a string is the distance between its points of support or " rest," musically speaking. Touching the frets of a guitar, for instance, is virtually shortening the string, and the frets are there not merely to serve as points of support, but also to secure that the string may be shortened by exactly the correct amount by means of the pressure of the player's fingers. In the piano, which is for that reason called a fixed instrument, a string of definite length, density, and tension is made to correspond to each note, and to give out the right number of vibrations when its key is struck.
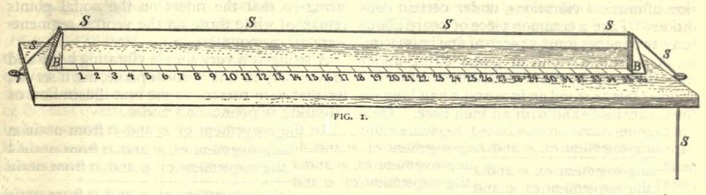
It is possible to bring about a visual expression of musical vibrations, under certain conditions. Take a common piece of board about forty-two inches long, a piece of fine brass wire, or, better still, a violin or guitar string about sixty inches long, a tape-measure, and two triangular bits of wood an inch and a half long on the vertical side and with an inch base. Tack the tape-measure on the board, beginning the yard three inches from the end of the board, or mark off thirty-six inches on it. Place a screw-eye at each end of the board at its middle point, and you are ready for a very simple experiment which will illustrate the point better than many words and elaborate figures.
Set up the two bridges, the vertical sides towards each other (Fig. 1), at the ends of the measured yard. Fasten the wire to one screw-eye, and, letting it pass over the two bridges and through the second screw-eye, weight it by fastening a flat-iron on the overhanging end.
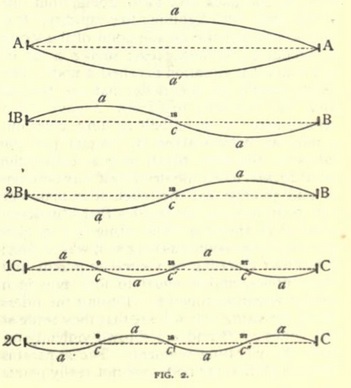
Having put some bits of paper cut in a Y shape astride the string, set the string into musical vibration by gently plucking it at its middle point. It will swing back and forth past the dotted line which indicates its position when at rest, taking positions AaA and Aa'A (Fig. 2) in rapid succession. The paper riders are thrown by the vibration.
Now touch lightly with the finger the point over the number 18 and pluck the string at 27. The light touch of your finger, or even of a feather, will serve as the fret does on the guitar --- there are now two strings practically half the former length. Instead of vibrating as a whole, like A, it first takes the position 1B, and then 2B, and back and forth, going from one to the other with lightning-like rapidity. It is easy to see that the middle point of the string is comparatively motionless ; such a point of rest in musical vibration is called a node. The riders remain on the node, but are thrown from the vibrating segments. A gave out a certain note ; B, being half as long, gives out a note an octave above A.
Again put the riders on the wire, touch with a feather the point 27, and pluck the string half- way between 27 and 36 (Fig. 1) ; the touch at 27 makes of that point a node, but besides that it makes a node at 18 and at 9. The string C (Fig. 2) is practically one-fourth as long as it was at first ; it has four vibrating or ventral segments and three nodes, and is equal to four nine-inch strings vibrating together. Putting the riders along the string you will see that they settle at the nodes cc'c" and are thrown violently off from the vibrating segments.
The apparatus is so rough that the nodes are not really points of rest, and the riders may not stay on, but the agitation is manifestly very much less at the nodes than on the ventral segments of the string. With the apparatus described I have succeeded a number of times in agitating the string so that the riders on the nodal points remained while those on the ventral segments were all dismounted.
A string is a very simple vibrating body and moves only in one vertical plane, but it serves, for that very reason, as the best illustration of vibrating segments and nodes.
In the movement of B and C from position 1 to 2 there is not the violent reversal that there appears to be --- the wave generated by the pull at a (1B and 1C) runs along the string to the end, and from that point it is reflected back in the direction 2B and 2C. If the attempt is made to touch the string, or dampen it, as it is technically called, at any point not an exact divisor of 36, the result would have been a joggle, not a vibration ; the wave would not have reached the far end of the wire in the right phase to be reflected back regularly.
So far we have only been considering the simplest vibrations, a single wave running back and forth on a string ; but in sound-waves, as in water-waves, motion is superposed upon motion, ripples upon waves, in an inconceivable complexity. If we could produce by the sonorous body only such simple vibrations as these we have been examining, all musical instruments, including the human voice, would sound exactly alike, so far as quality is concerned. The only possible difference would be in range and intensity. We could not distinguish the notes of a French horn from those of a guitar. Simple vibrations constitute only the fundamental tone, which is the same for the identical note on all musical instruments.
Tyndall in his book on sound says : "It has been shown by the most varied experiments that a stretched string can either vibrate as a whole, or divide itself into a number of equal parts, each of which vibrates as an independent string. Now it is not possible to sound the string as a whole without at the same time causing, to a greater or less extent, its subdivision ; that is to say, superposed upon the vibrations of the whole string we have always, in a greater or less degree, the vibrations of its aliquot parts. The higher notes produced by these latter vibrations are called the harmonics of the string. And so it is with other sounding bodies; we have in all cases a coexistence of vibrations. Higher tones mingle with the fundamental one, and it is their intermixture which determines what, for want of a better term, we call the quality of the sound." And again, later on, he says: "Pure sounds without overtones would be like pure water, flat and dull. The tones, for example, of wide-stopped organ-pipes are almost perfectly pure But the tones of such pipes, though mellow, would soon weary us ; they are without force or character, and would not satisfy the demand of the ear for brightness and energy. In fact, a good musical clang requires the presence of several of the first overtones. So much are these felt to be a necessity that it is usual to associate with the deeper pipes of the organ shorter pipes which yield the harmonic tones of the deeper one. In this way, where the vibrating body itself is incapable of furnishing the overtones, they are supplied from external sources." In fact, the ear demands that each note shall be a harmonic chord, powerfully dominated by the fundamental tone though it may be.
The determining value in the overtones of an instrument was felt, practically, long before their existence was known in theory. Makers of musical instruments learned long ago how to quench certain objectionable overtones, even before they knew just what they were doing.
Imagine what the air would look like if it could be made visible when an orchestra is setting it into vibration, with thousands of tones and their attendant overtones crossing and recrossing with infinite complexities of form. The different notes are not each making its separate mark, but all have combined, helping or hindering one another, and coming as a single full harmony to the ear, where there is a resolution of the composite movement ; and this marvelous "lute of three thousand strings" takes up the tangled skein of sound, separates it into its constituent tones, and conveys them separately to the brain.
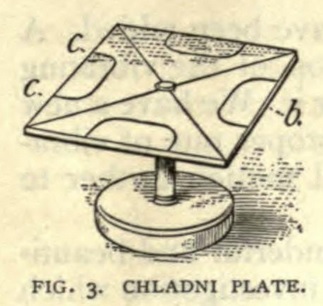
The idea of getting a visual expression for musical vibrations occurred to Chladni, a physicist of the last century. He fastened a plate of glass by its center, and then, having scattered some sand over the surface, threw it into sonorous vibrations by means of a violin bow. Imagine the delight with which he saw the sand stir and form into line on the plate, forming a star of twelve rays.
Square plates of glass or metal screwed or even glued to a central support can be made by the merest tyro with tools, and give wonderful results (Fig. 3). A plate, like a string, has one rate of vibration which belongs to it, but again, like a string, by "dampening" it with a touch of the finger or fingers in different points along the edge the note changes and with it the figure made by the sand. The lines on the plate where the sand settles are the nodes, the lines of comparative rest. The violent agitation in the parts left bare can be shown by mixing a little lycopodium powder with the sand ; this is excessively light, and is caught in the little whirlwinds of air generated about the vibrating segments.
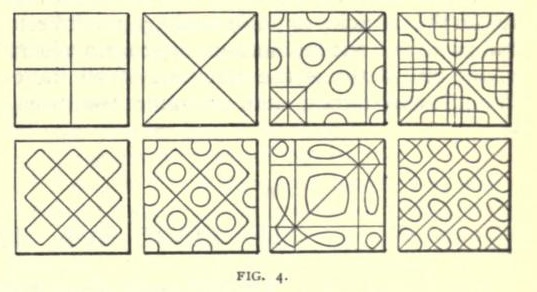
The marvelous intricacy of the vibrations of these plates may be seen from a few figures given above, which indicate the lines taken by the sand when certain notes were sounded on the plate (Fig. 4).

A little instrument invented by Professor Sedley Taylor, and called the phoneidoscope, gives a most exquisite illustration of music made visible. It consists of a tube which terminates in a hollow cup or funnel-shaped enlargement ; over the mouth of this funnel a thin sheet of metal or pasteboard with a smooth-edged and symmetrical opening is made. Across the opening a film of soap-suds is drawn and left to stand till colors begin to form. These soap-bubble colors, as is very well known, are due to the thickness of the film. In an ordinary soap-bubble they flit over the surface irregularly. This is because from the exposed outer surface of the bubble, and the irregular force which is expanding it from within, the film is always varying in thickness. The colors tell inexorably just how much this variation is at every point of the surface. A special fluid, made very carefully, is necessary for experiments with the phoneidoscope, because the soap-film must thin sufficiently to show bright colors and yet be strong enough to stand the vibrations into which it is thrown by the voice.

When the colors are well established in the film a sustained musical note should be sung into the open end or mouthpiece of the tube, using care not to breathe or blow into it. The colors begin to move, and, if the note is sustained, whirl into the most beautiful gyrating figures.
Mr. [Emil] Behnke, in a discussion before the Musical Association of England, [Proceedings 13, 143 (1888)], says : "I have for many years tried to get what help I could from science in the treatment of the human voice, and when Professor Sedley Taylor some years ago brought this phoneidoscope under my notice I was very highly delighted. He told me it would be possible by means of a soap-film to get different figures for different pitches, for different intensities, and for different qualities of tone. . . . I did not find the phoneidoscope answer in practice. In the first place there was great difficulty about these films, which would continually burst. In the second place there was no doubt I did get a variety of figures, and not only that, but a variety of exceedingly beautiful colors. The experiments were most fascinating ; but I did not get the same figures regularly for the same changes in either pitch or intensity or quality, and therefore, so far as practical results were concerned, the instrument was of no use. ... Of course it does not follow because we have not yet succeeded in these matters we never shall."
We are now upon the very threshold of Mrs. Hughes's voice-figures ...
[Threshold ? It seems rather odd that Herrick does not mention the context of Behnke's remark above ; it was delivered in the general discussion after a presentation by Hughes, and continues: "I am very much interested in Mrs. Hughes' paper, and it seems to me that everybody connected with the production of the voice in any shape or form ought to do whatever is possible to further these experiments and to assist in them, because I am quite sure that we are only at the threshold of these discoveries." Behnke, his wife, and his daughter were probably the best-known speech-therapists of the late Victorian and Edwardian periods.]
We are now upon the very threshold of Mrs. Hughes's voice-figures, and have reached it by the same path which brought her to them in the first instance. Her eidophone is constructed on the same principle as the phoneidoscope : instead of the frail lamina of soap-suds she has a stretched membrane of india-rubber to receive the vibrations, and on this is spread a thin layer of some pasty substance which will retain the record made by the vibrations of the membrane.
These voice-flowers are not the simple visual forms corresponding with the vibrations of the air set in motion by the voice. The waves generated in the closed bowl of the eidophone are reflected again and again from the sides of the vessel. The volume of air inclosed has its own rate of vibration; the stretched membrane has also its own rate, which in turn is modified by the character and thickness of the paste spread upon it. Added to these are molecular forces of cohesion and adhesion between the particles of paste, and again between the paste and the membrane. The form which grows into shape is the resultant of all these complicated forces, and, in some instances, new elements of change have been added. A glass plate is placed on top of the vibrating membrane and moved over it. We have a new body introduced with its proper rate of vibration, besides a mechanical motion further to complicate the problem.
The results are very wonderful and beautiful, and open up a field for investigation which is most interesting, but so far we have the resultant of many forces, not one of which has been weighed and measured. In a letter from Mrs. Hughes, replying to some questions asked in the hope of greater accuracy, she says: "The notes producing the figures vary necessarily with the weight of material used and the tension of the membrane, so that any one note may, under different circumstances, produce different figures, and, conversely, different notes may, under different circumstances, produce similar figures."
The daisy forms were sung into shape, she says, by extremely low notes very softly sounded, some of them by A in the first space of the bass clef --- a wonderful note to be reached by a woman's voice, whose highest note is the B-flat above the treble clef, a compass of over three octaves ! Sometimes geometrical forms not given in the illustrations were produced by the highest notes of her voice, while the serpent, fern, and tree forms were made by singing her middle notes with great intensity.
Mrs. Hughes is first of all a singer, and to further her voice culture she entered upon the series of experiments in which she has shown infinite patience and skill. That her experiments are amateurish rather than scientific is no discredit, for she has opened up a new field into which the scientist may enter and reach results of great interest and value.
Sophie B. Herrick.
Herrick's discussion of standing waves is excellent, comparable to what one would find in any textbook today. But it also reveals a certain bias -- the complexity of the system and the curious organic quality of Hughes's "voice figures" are only defects if one insists on the importance of reductionism and the superiority of simple geometric shapes known to the Greeks over intricate "fractal" arabesques. Chladni and his school, as we will see next time, did not exactly share this bias ...
SINGING IN CHLADNI'S GARDEN