(The present article is copied from a printed paper, which I [presumably William Nicholson, editor of the journal] obtained from Messrs. Johnson and Co., booksellers, in St. Paul's Church-yard. This boy has been publicly exhibited in America and in London, and some time ago subscriptions were solicited for placing him to be educated under the inspection and care of several mathematical gentlemen : but I have been informed, that the plan was relinquished, from some reasons on the part of his father ; and he is again to be seen by the public. A subscription is now solicited for publishing a portrait of him on the following terms) :
ZERAH COLBURN, a child just eight years of age, without any previous knowledge of the common rules of arithmetic, or even of the use and power of the Arabic numerals, and without having given any particular attention to the subject, possesses (as if by intuition) the singular faculty of solving a great variety of arithmetical questions by the mere operation of the mind, and without the usual assistance of any visible symbol or contrivance.
This print will be engraved from a drawing by Mr. Trumbull ; and the size of it will be about 12 inches by 10.
The price to subscribers will be One Guinea, to be paid at the time of subscribing : and the plates will be delivered according to the order of subscription.
The following gentlemen (who are well acquainted with the extraordinary abilities of this child) have kindly undertaken to attend to the progress and execution of the work, and to see to the distribution of the plates, viz.
- Sir James Mackintosh [social scientist and political reformer]
- Dr. W. H. Wollaston, Sec. R. S. [discoverer of palladium and rhodium]
- William Vaughan, Esq. [scientifically-inclined merchant who re-engineered and modernised the port of London]
- John Bonnycastle, Esq., Math. Prof. [at the Royal Military Academy]
- Francis Wakefield, Esq. [probably the Nottinghamshire merchant and philanthropist who assisted Coleridge]
- William Allen, Esq., F. R. S., F. L. S [Quaker scientist and abolitionist]
- John Guillemard, Esq., F. R. S., F. Amer. S. [scientist remembered chiefly as a member of the commission that tried to settle international financial disputes caused by the American Revolution]
- Samuel Parker, Esq.
- Francis Bailey, Esq. [probably Francis Baily, the astronomer remembered today for having noticed the dramatic highlighting of mountains on the limb of the Moon during a solar eclipse.]
[If I have identified them correctly, these men all belonged to the same social set, which also included the Wedgwoods, the Darwins, and Charles Babbage. Most if not all of them were what Gibson and Sterling have called "Industrial Radicals", pro-science Romantics who hoped that technological advances would lead to deep social changes and the collapse of the old order.]
Subscriptions are received by either of the above gentlemen, or by Messrs. Johnson and Co., No. 72, St. Paul's churchyard : and printed receipts will be given for the same, which must be produced and given up at the time the plates are delivered.
Zerah Colburn is at present to be seen at the Exhibition Rooms, Spring Gardens. Many persons of the first eminence for their knowledge in mathematics, and well known for their philosophical inquiries, have made a point of visiting him : and they have all been struck with astonishment at his extraordinary powers. It is correctly true, as stated of him, that --
"He will not only determine, with the greatest facility and dispatch, the exact number of minutes or seconds in any given period of time; but will also solve any other question of a similar kind.
"He will tell the exact product arising from the multiplication of any number, consisting of two, three, or four figures, by any other number consisting of the like number of figures.
"Or, any number, consisting of six or seven places of figures, being proposed, he will determine, with equal expedition and ease, all the factors of which it is composed.
"This singular faculty consequently extends not only to the raising of powers, but also to the extraction of the square and cube roots of the number proposed ; and likewise to the means of determining whether it be a prime number (or a number incapable of division by any other number) ; for which case there does not exist, at present, any general rule amongst mathematicians."
All these, and a variety of other questions connected therewith, are answered by this child with such promptness and accuracy (and in the midst of his juvenile pursuits) as to astonish every person who has visited him.
At a meeting of his friends, which was held for the purpose of concerting the best method of promoting the views of the father respecting his education, this child undertook, and completely succeeded in, raising the number 8 progressively up to the sixteenth power : and in naming the last result, viz. 281,474,976,710,656, he was right in every figure.
He was then tried as to other numbers, consisting of one figure ; all of which he raised (by actual multiplication and not by memory) as high as the tenth power : with so much facility and dispatch, that the person appointed to take down the results was obliged to enjoin him not to be so rapid.
With respect to numbers consisting of two figures, he would raise some of them to the sixth, seventh, and eighth power ; but not always with equal facility : for the larger the products became, the more difficult he found it to proceed.
He was asked the square root of 106,929, and before the number could be written down, he immediately answered 327. He was then required to name the cube root of 268,336,125, and with equal facility and promptness he replied 645. Various other questions of a similar nature, respecting the roots and powers of very high numbers, were proposed by several of the gentlemen present, to all of which he answered in a similar manner.
One of the party requested him to name the factors which produced the number 247,483, which he immediately did by mentioning the two numbers 941 and 263 ; which indeed are the only two numbers that will produce it. Another of them proposed 171,395, and he named the following factors as the only ones that would produce it ; viz. 5 × 34,279 ; 7 × 24,485 ; 59 × 2,905 ; 83 × 2,065 ; 35 × 4,897 ; 295 × 581 ; and 413 × 415.
He was then asked to give the factors of 36,083 ; but he immediately replied that it had none ; which in fact was the case, as 36,083 is a prime number. Other numbers were indiscriminately proposed to him, and he always succeeded in giving the correct factors, except in the case of prime numbers, which he discovered almost as soon as proposed.
It had been asserted and maintained by the French mathematicians, that 4,294,967,297 ( = 1 + 232) was a prime number: but the celebrated Euler detected that errour by discovering, that it was equal to 6,700,417 × 641. The same number was proposed to this child, who found out the factors by the mere operation of his mind.
One of the gentlemen asked him how many minutes there were in forty-eight years ; and before the question could be written down, he replied 25,228,800 ; and instantly added, that the number of seconds in the same period was 1,513,728,000. Various questions of the like kind were put to him ; and to all of them he answered with nearly equal facility and promptitude ; so as to astonish every one present, and to excite a desire that so extraordinary a faculty should (if possible) be rendered more extensive and useful.
It was the wish of the gentlemen present to obtain a knowledge of the method by which the child was enabled to answer, with so much facility and correctness, the questions thus put to him : but to all their inquiries upon this subject (and he was closely examined upon this point) he was unable to give them any information. He positively declared (and every observation that was made seemed to justify the assertion) that he did not know how the answers came into his mind.
In the act of multiplying two numbers together, and in the raising of powers, it was evident (not only from the motion of his lips, but also from some singular facts which afterward occurred,) that some operation was going forward in his mind ; yet that could not (from the readiness with which the answers were furnished) be at all allied to the usual mode of proceeding with such subjects : and moreover, he is entirely ignorant of the common rules of arithmetic, and cannot perform, upon paper, a simple sum in multiplication or division.
But, in the extraction of roots and in mentioning the factors of high numbers it does not appear that any operation can take place ; since he will give the answer immediately, or in a very few seconds, where it would require, according to the ordinary method of solution, a very difficult and laborious calculation : and moreover, the knowledge of a prime number cannot be obtained by any known rule.
It may naturally be expected, that these wonderful talents, which are so conspicuous at this early age, will by a suitable education be considerably improved and extended ; and that some new light will eventually be thrown upon those subjects, for the elucidation of which his mind appears to be peculiarly formed by nature, since he enters into the world with all those powers and faculties, which are not even attainable by the most eminent at a more advanced period of life.
Every mathematician must be aware of the important advantages, which have sometimes been derived from the most simple and trifling circumstances ; the full effect of which has not always been evident at first sight. To mention one singular instance of this kind : The very simple improvement of expressing the powers and roots of quantities by means of indices introduced a new and general arithmetic of exponents ; and this algorithm of powers led the way to the invention of logarithms, by means of which all arithmetical computations are so much facilitated and abridged.
Perhaps this child possesses a knowledge of some more important properties connected with this subject ; and although he is incapable at present of giving any satisfactory account of the state of his mind, or of communicating to others the knowledge which it is so evident he does possess, yet there is every reason to believe, that, when his mind is more cultivated and his ideas more expanded, he will be able not only to divulge the mode by which he at present operates, but also point out some new sources of information on this interesting subject.
The profits of the present print will be given to the father of this child, in order to enable him to provide a more suitable education for his son : and it is hoped that the friends of science, and the public in general, will promote a plan, which promises to be attended with such advantages.
[The portrait of Colburn promoted by the above circular, if it was ever created, does not survive.
Readers may be puzzled by the statement "It had been asserted and maintained by the French mathematicians, that 4,294,967,297 was a prime ..."Why was this particular number of interest?
"Generalised Fermat numbers" are numbers of the form
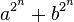
where a, b, and n are positive integers. Fermat himself, writing in 1640, considered only the case a = 2, b = 1 ; he noticed that the first five examples are prime, and believed that he had found a recipe for generating an unlimited number of increasingly large primes. But arithmetic was hard work in the Seventeenth and Eighteenth Centuries. It was not until 1732 that someone (Euler, as it happened) actually computed the sixth number in the series, and realised that it could be factored. Indeed, all of the original Fermat numbers after the fifth which have been computed have turned out to be composite.
Despite this disappointment, the Fermat numbers have remained of enormous interest to number theorists for four centuries both because of their many strange and unexpected properties -- for example, Gauss showed that a regular polygon can only be inscribed in a circle by ruler-and-compass construction if the number of its sides is a power of two times a product of Fermat primes! -- and because some unusually simple tests exist to determine whether they are prime without actually factoring them. The latter feature has been exploited in the modern quest for large prime numbers, a subject which is suddenly of great practical importance in the Information Age. Interested readers should consult Chris Caldwell's excellent website The Prime Glossary.]