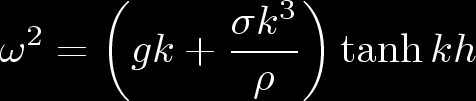
The topic of 8.981 will be gravitational waves. Contrary to some material floating out there, the topic will not be gravity waves. Since some people might have an interest in "gravity waves," here is a brief description:
"Gravity waves" (commonly referred to as "water waves") are modes excited in an incompressible fluid. One source of restoring force is provided by gravity (hence "gravity waves"); a second is provided by surface tension. The dispersion relation of these waves is given by
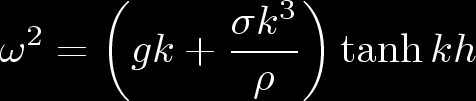
where k is the wavenumber, rho is the fluid density, sigma is the fluid's surface tension, and h is the water's depth.
For water, rho = 1 gm/cm3; at 20 degrees C and standard atmospheric pressure, the surface tension of the water/air interface is 73 gm/sec2. The gravity and surface tension terms are thus roughly equal at a wavelength of about 1.7 cm; the gravity term dominates for longer wavelengths. This is the regime of "gravity waves" proper.
In deep water, kh >> 1; the hyperbolic tangent limits to 1, and the dispersion relation becomes
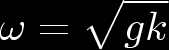
The phase and group velocities are given by vphase = 2vgroup = (g/k)½. Note that long wavelength modes have higher group velocity than short wavelength modes.
In shallow water, kh << 1, it usually suffices to take the first two terms in the expansion of the hyperbolic tangent:

In very shallow water, the second term can be neglected and the waves are non dispersive.
This discussion was adapted from the text Vibrations and waves in physics, by Iain G. Main.
It's worth emphasizing that being super careful with this nomenclature is not just anal retentive; it can in fact be very confusing to confuse the two. For example, "gravity waves" of the type discussed here can occur in the fluid that constitutes a neutron star. In such a circumstance, you can actually have "gravitational waves" arising from "gravity waves"!