r100_a0.95_lz0.5

The results given here are for an orbit at r/M = 100, a/M = 0.95. To make the orbit inclined, I started with the z-component of angular momentum needed to make a prograde, equatorial orbit and cut that angular momentum in half. I then solved for the energy and Carter constant needed to produce a stable circular orbit. The following table summarizes the resultant orbital characteristics, and the characteristic effects of radiation reaction on that orbit. These results include multipoles from l = 2 to l = 6.

Orbit 
quantities
Energy
0.9950344
z-component of 
angular momentum (Lz)
5.062587
Carter constant
77.17104
iota
60.04534 degrees
iota'
59.95326 degrees
Omega_phi
1.000358 × 10-3
Omega_theta
9.985256 × 10-4
 
Radiation 
reaction 
quantities
Energy flux to infinity
-6.219403 × 10-10
Energy flux down the horizon
+1.919636 × 10-15
Lz flux to infinity
-3.117506 × 10-7
Lz flux down the horizon
+2.860425 × 10-12
Rate of change of radius
-1.261018 × 10-5
Rate of change of Carter constant
-9.461233 × 10-6
Rate of change of inclination angle
+1.204036 × 10-10
 

All of these quantities are in non-dimensional units. To get to physical units, apply the following rules:

  • Multiply the energy by mu (where mu is the mass of the orbiting particle); multiply the angular momentum by mu M (where M is the black hole mass); multiply the Carter constant by mu2 M2.

  • Divide the frequencies by M.

  • Multiply rate of change of energy by (mu/M)2; multiply rate of change of angular momentum by mu2/M; multiply rate of change of Carter constant by mu3.

  • Multiply rate of change of radius by (mu/M).

  • Multiply rate of change of inclination angle by (mu/M2).

    Note that the inclination angle increases, as predicted by Fintan Ryan [Phys. Rev. D 52, R3159 (1995)]. Fintan's formula is an expansion in both 1/r and a, and so we expect that it should agree fairly well with the numerical result shown here (leading cause of disagreement is likely to be due to the large value of a). Indeed, Fintan's prediction for this orbit is 1.34 × 10-10, off by about 10%.

    In a different paper, Fintan gives the rate of change of radius for inclined orbits [Phys. Rev. D 53, 3064 (1995)]; his prediction for this orbit is -1.28 × 10-5, off by only 1.5% from the numerical result.

    Note also that the energy and angular momentum flux from the horizon is positive, i.e. the particle's energy and angular momentum increase due to radiation falling into the horizon. This is due to superradiant scattering: radiation is scattered by the hole's ergosphere, absorbing some of the energy stored in the spin of the spacetime, and then gives a "kick" to the orbiting particle.

    Here's what the waveform looks like at this point in the particle's evolution:

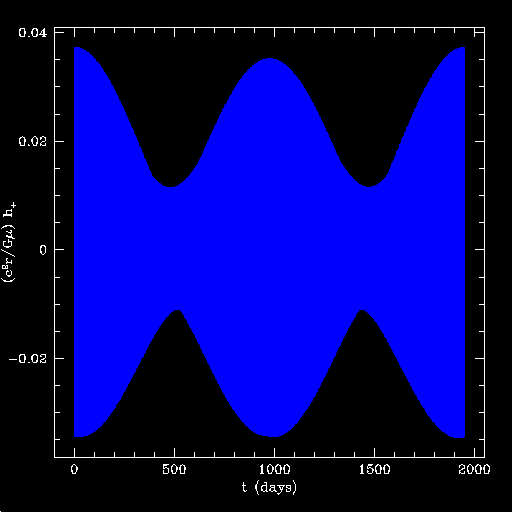
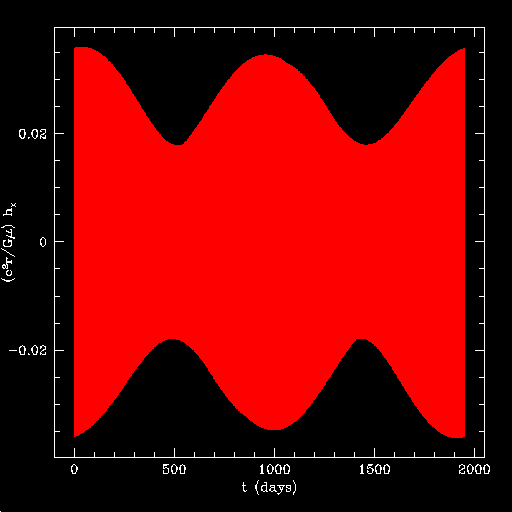
    This waveform is observed in the hole's equatorial plane. The blue lines are h+, the red lines h×. The low-frequency amplitude modulation is due to Lense-Thirring precession, i.e. the dragging of the orbit's nodes by the black hole's spin. The frequency of this modulation is 2 × (Omegaphi - Omegatheta) = 3.66 × 10-6 M-1. This difference is rather small in this weak-field region; thus, orbital precession is rather slow, and there are many cycles in each peak.

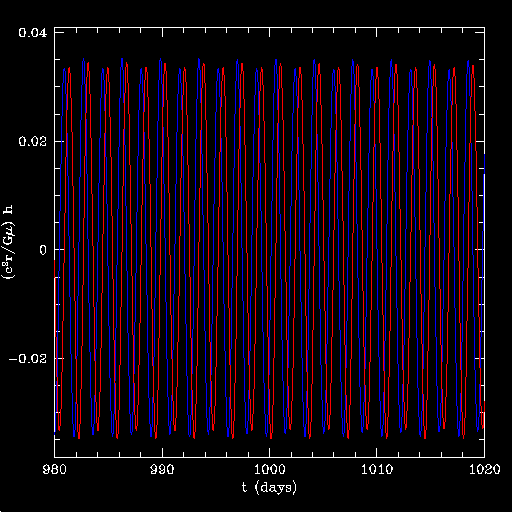
    Here's a zoom on one of the peaks. Notice that the signal is practically monochromatic aside from the precession induced modulation.

    The radiated energy has the following distribution:

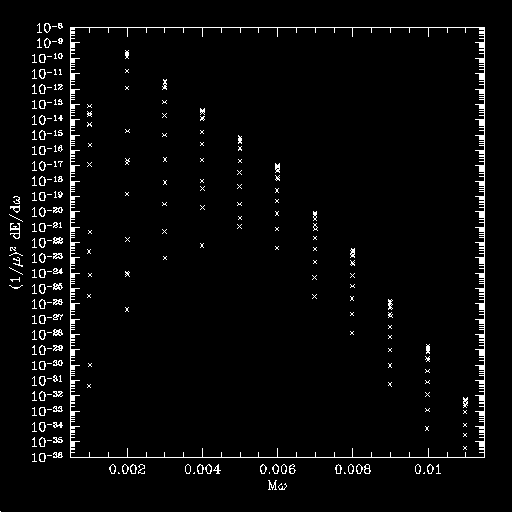
    This is fairly narrow; notice that there is no noticeable break in the rate with which the energy falls off. This is consistent with the spectrum for a = 0.95M, r = 7M.