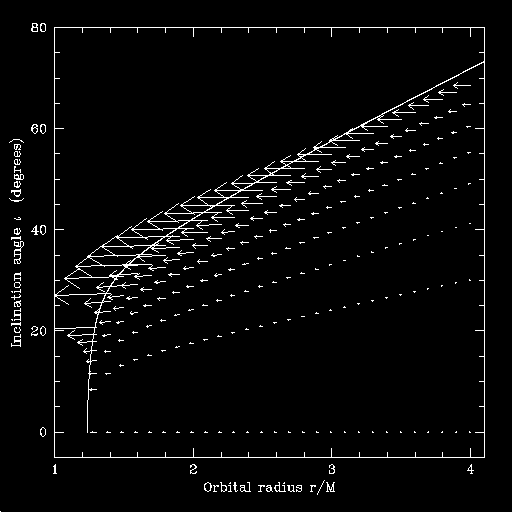
First, here's a plot showing the evolution vectors - the direction in r and iota in which the orbit is driven:

The line in this plot gives the angle at each radius of the least-bound stable orbit; orbits at higher inclination angle are unstable, and so are astrophysically irrelevant. The tail of each arrow gives the (r, iota) coordinates of a particular orbit. The arrow points in the direction to which radiation reaction pushes the arrow, and the length is proportional to the rate at which the evolution occurs.
Using this field of data points, I evolve a set of orbits. The orbits start at r/M = 4 and various values of iota. I use cubic spline interpolations to find the values of dr/dt and d(iota)/dt at arbitrary coordinate points, given the field of data shown above.
Here is a set of inspiral trajectories computed for a 1 solar mass body spiraling into a 106 solar mass black hole:
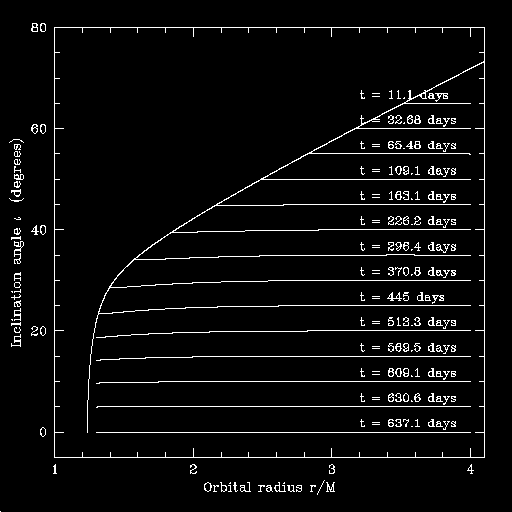
The time given at each trajectory is the number of days it takes to spiral from 4M to the last stable orbit. (I actually stop at either the LSO or 1.3M, whichever comes first. It's hard to make a data set that densely samples very close to the LSO.)
This next plot is essentially the same as that given above, but, in the process of computing the inspiral trajectory, I ignore the radiation that goes ``down the horizon'': evolution in the following plot is driven solely by radiation to infinity:
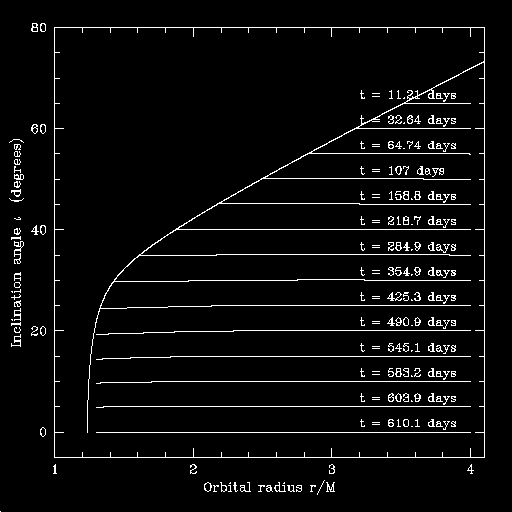
The numbers are quite a bit different! In particular, for orbits that are not sharply tilted, the ``horizon radiation'' prolongs the inspiral. This result follows from the fact that the quantities representing the flux of radiation down the horizon can be recast as quantities describing the tidal distortion of the horizon. The ``horizon bulge'' gets dragged ahead of the orbiting body when the hole spins rapidly. The torque from that bulge thus increases the orbital velocity.
Here are the same plots, parameterized by the number of orbital cycles rather than the inspiral time. First, including the horizon flux:
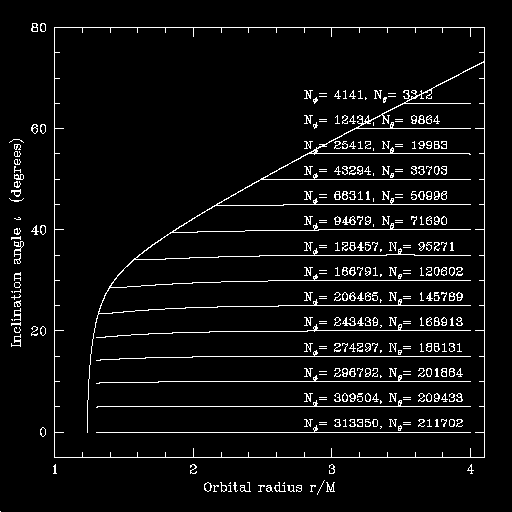
Second, ignoring the horizon flux:
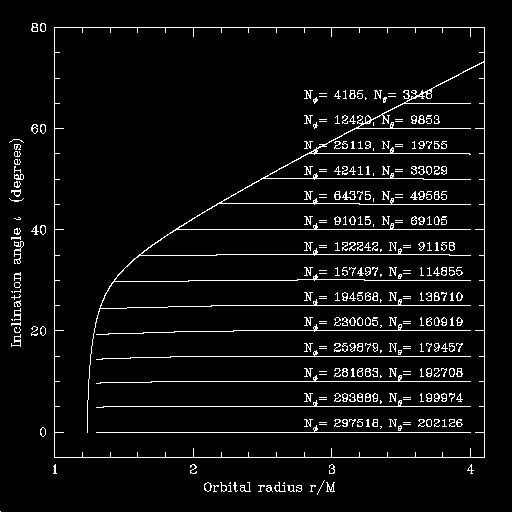
Particularly for shallow orbital inclination, the difference in the number of cycles is huge - 104 or more. This demonstrates the importance of including the down horizon flux: it is an enormous effect. These inspirals are strongly stamped by the strong-field features of black hole spacetimes.
Last modified 13 April 2001.