 The Heliosphere
The Heliosphere The Heliosphere
The Heliosphere
Space Science Lab/ES82
NASA Marshall Space Flight Center
Huntsville, Alabama 35812 U.S.A.
[This is a slightly expanded version of a paper which appeared in EOS December 1994]
The first suggestions concerning the existence and nature of the heliosphere were made in 1955 by Leverett Davis in connection with the origin and propagation of cosmic rays. The essential element was that "solar corpuscular radiation" (termed the "solar wind" in 1958 by Eugene Parker) would force matter and magnetic flux in the local interstellar medium outward, thereby partially excluding cosmic rays. The simplest expression of the concept is that the solar wind blows a spherical bubble, the "heliosphere," that continually expands over the lifetime of the solar system. However, if there is a significant pressure in the interstellar medium, the expansion must eventually stop. The resulting quasi-static bubble is then of the order R AU where R is determined by equating the ram pressure of the solar wind to the total interstellar pressure, P (internal + dynamic + magnetic + cosmic ray pressure):
(1)
Here n is the ion number density at 1 AU, m the average ion mass, and V the speed of the solar wind. It is implicit in this relationship, essentially the same as used currently, that the solar wind is highly supersonic and therefore the left hand side of equation (1) need contain only the solar wind ram pressure. Davis, using what little information was available 40 years ago, suggested R = 200 - 2000 AU.
In the above there are several gross simplifications. For example, if the heliosphere were in a steady state (likely since R/V ~ 1-100 years) what happens to the accumulated solar wind plasma and magnetic field? How does the solar wind feel the presence of the interstellar medium? What happens if the interstellar plasma is moving with respect to the Sun? These questions can be dealt with quite easily and in doing so one arrives at our present understanding of the heliosphere.
First, supersonic solar wind flow must terminate at a standing inwards-facing
shock wave if the interstellar pressure is not zero. This is because the
presence of the interstellar medium cannot be communicated to the supersonic
solar wind, and conservation of mass and pressure balance require that the
solar wind flow be slowed as it meets the interstellar medium. As a consequence
the interpretation of equation (1) must be modified so that R refers to
the distance to the shock. The flow downstream of the shock is subsonic and the
total pressure is therefore nearly uniform. Taking n = 8
protons per cubic centimeter, V = 400 km/s and
(allowing for the presence of helium), we find that
R ~ 85 AU for
, using a slightly more
detailed form of (1) [Suess,
1990]. This interstellar pressure corresponds to a magnetic
field, BI, of 0.6 nT, if other contributions to P are neglected. Current
estimates favour a
slightly smaller value for BI, but this is compensated to some extent by other
effects and the minimum distance to the termination shock is probably on the
order of 100 AU.
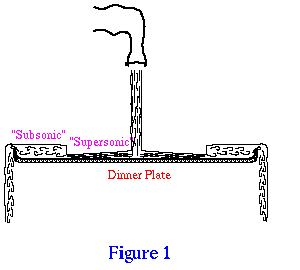
Much of the physics requiring the existence of the shock is analogous to the flow of a fluid over a surface in the presence of gravity. If one allows a steady stream of water from a faucet to impinge on a horizontal dinner plate, it will be observed that the water flows radially away from the point of impact at "supersonic" speed. [The latter is evident from the standing waves produced by any obstacle in the flow.] Provided the flow rate is not too large, a hydraulic jump or shock wave is produced at a position such that the water outside the shock is just deep enough to flow over the raised edge of the plate. It is easy to demonstrate that the flow is "subsonic" in this region. Figure 1 is a cartoon of this phenomenon. In this analogy, the depth of the water should be compared with the pressure/density of solar wind plasma.
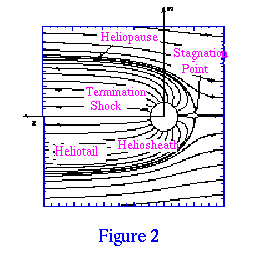
The motion of the Sun and the heliosphere relative to the matter comprising the very local interstellar medium (VLISM) is the next issue. It is natural to assume that the relative velocity might be parallel to the motion of the Sun with respect to the nearer stars, namely from the solar apex (right ascension ~ 271 degrees, declination ~ 30 degrees) with a speed of ~ 20 km/s. However, typical interstellar clouds have random (line of sight) velocities of ~ 10 km/s or more and the direction could easily be 30 degrees or more from the solar apex - which turns out to be the case, as we describe below. Furthermore, with such speeds it would only require a plasma ion density in the VLISM of 0.5 per cubic centimeter for the ram pressure to be the same as that of a magnetic field of 1 nT (giving R = 50 AU): hence the motion of the VLISM should be taken into account. The simplest model of the resulting stagnation point flow is found by assuming incompressibility and neglecting magnetic fields. The streamlines in such a model are shown in Figure 2.
 Larger version of Figure 2 (10K)
Larger version of Figure 2 (10K)
The interstellar flow turns at the stagnation point to go around the heliosphere and the subsonic solar wind flow is turned in the "heliosheath" between the termination shock and the heliopause to flow down the "heliotail." The solar wind inside the termination shock is flowing supersonically and radially. The terminology has been chosen to be closely analogous to that for the Earth"s magnetosphere because of the topological similarity of the two configurations.
Until 1972 most observations of the VLISM involved averages over distances of 100 parsecs or more. From the observations of Faraday rotation and dispersion of pulsar emissions, it was deduced that the average electron density is ~ 0.03 per cubic centimeter and the magnetic field strength is ~ 0.3nT, with large fluctuations of the same order. Radio observations of the 21 cm interstellar line suggested density of neutral hydrogen on the order of 0.7 per cubic centimeter, considerably higher than the value obtained from measurements of Lyman alphalpha absorption in the spectra of nearby early type stars, namely about 0.1 per cubic centimeter.
We do not presently have significantly better values for the electron density and magnetic field strength, but the situation with regard to neutral hydrogen and helium has greatly improved. Observations made from the spacecraft OGO 5 led to the remarkable result that interstellar neutral hydrogen is detectable as a consequence of the backscattering of solar Lyman alpha within ~ 5 AU and that the direction of approach is not from the solar apex but close to the projection of the apex direction onto the ecliptic plane. The heliocentric distance of penetration is determined easily by measuring the parallax of the Lyman alpha emission from observations made from the vicinity of the Earth at different times during the year.
The forces acting on a neutral hydrogen atom approaching the Sun are gravity and the radiation pressure. In addition, atoms are lost, mainly as a result of charge exchange with solar wind protons which converts a fast solar wind proton into a fast hydrogen atom. The proton of interstellar origin is "picked up" by the interplanetary electric and magnetic fields. The heliocentric distance to which interstellar atoms having a relative speed of ~ 20 km/s can penetrate before the probability of loss by charge exchange becomes high is about 4 AU, corresponding roughly to the distance obtained from the OGO 5 parallax measurements.
The brightness distribution of scattered solar Lyman alpha corresponding to a given neutral hydrogen density distribution can be computed and compared with observations, provided one knows the shape of the solar Lyman alpha emission line. However, it is not easy to determine the inflow speed of the neutral beam, U, and the loss mean free path, lambda, separately. Hence the value deduced for U is rendered uncertain by the uncertainties in evaluating lambda.
For the case of interstellar neutral helium the situation is different because radiation pressure has negligible effect and the value of lambda is such that the neutral beam penetrates to well within 1 AU if U~ 20 km/s. The interesting conclusion that can be drawn from measurements of scattered solar HeI 584 Å radiation is that the maximum intensity should occur in the downwind direction, looking along the accretion axis, rather than in the upwind direction as in the case of hydrogen. This provides a straightforward means of determining the direction of the interstellar wind.
The early results from observations of scattered Lyman alpha and HeI 584 have been confirmed and refined by the neutral helium experiment on Ulysses and by direct observation of pickup ions on AMPTE. Very accurate values have been found for the speed and direction of the helium wind together with a good value for the temperature. These concensus results are given in Table 1. With regard to the cosmic ray pressure in Table 1, the heliosphere is near a bubble of hot gas, evidently recent and not necessarily in equilibrium as far as locally produced cosmic rays are concerned, so it is possible that a low energy component exists locally and contributes to the total pressure. If this does happen, the shock itslef will be thickened and made more turbulent in the course of the interaction.
Returning to the interstellar pick-up ions, they have an interesting fate. After entering the heliosphere initially as neutral atoms, being ionized, and then picked up, they are carried out to the termination shock. There, a small percentage are accelerated to cosmic ray energies and then propagate back into the inner heliosphere where they are observed as "anomalous cosmic rays." This process has recently been confirmed by the observervation on AMPTE and Ulysses that anomalous cosmic rays are, indeed, singly ionized.
With regard to interstellar plasma, soft x-ray observations suggest that the Sun is located within an irregular region of hot (~ million degree K), low density (~ 0.05 per cubic centimeter) plasma with dimensions of the order of tens to hundreds of parsecs. This "local bubble" of hot plasma must have been produced by a combination of one or more supernovae and stellar winds associated with a group of O and B stars. However, it is quite clear that the VLISM does not have the same characteristics as the local bubble material as a whole since it contains neutrals having a temperature of only ~ 7000 K. The Sun is usually considered to be immersed in a region of "local fluff" that is relatively cool and dense. Since one would expect to have pressure balance between the fluff and the hot medium it would seem to be necessary that the former contains an unobservable component of plasma and magnetic field which would have p/k ~ 10,000 degrees K per cubic centimeter to compensate for the very low pressure of the observed neutrals described above (p/k < 10,000 degrees K per cubic centimeter). This seems rather too large unless the pressure is mainly magnetic which would require BI ~0.6nT. The plasma alone would have to have n >1 per cubic centimeter to be able to produce such a hydrostatic pressure and its ram pressure would put the solar wind termination shock at R ~ 30AU, whereas direct observation places it beyond 50 AU. The relative abundances of hydrogen and helium atoms in the VLISM given in Table 1 suggest that the density of the ionized component (mainly protons) is not greater than about 0.3 per cubic centimeter. If the termination shock is assumed to ie at ~ 100 AU, more reasonable values for the density (~ 0.1per cubic centimeter) can be accomodated if there is also a significant magnetic field (B~ 3-5nT) and this can provide a match to the hydrostatic presure in the local bubble if the latter has been slightly over-estimated by say a factor of 2.
Table 1. Properties of the Very Local Interstellar Medium
Property Value
NEUTRAL COMPONENT
Flow Speed 25 +/- 2 km/s
Flow Direction 75.4 ecliptic longitude
-7.5 ecliptic latitude
Hydrogen density 0.10 +/- 0.01 /cubic cm
Helium density 0.010 +/- 0.003 /cubic cm
Hydrogen temperature (7 +/- 2) x 1000K
Helium temperature (7 +/- 2) x 1000K
IONIZED COMPONENT
Electron density < 0.3/ cubic cm
Flow speed Assumed same as neutral component
Flow direction Assumed same as neutral component
Ion temperature Assumed same as neutral component
MAGNETIC FIELD
Magnitude 0.1 - 0.5 nT
Direction Unknown
COSMIC RAYS
Total pressure (1.3+/-0.2) x 10^(-12)dynes/square cm
The collision time between interstellar neutral atoms and ions is ca. 1000 years and the mean free path is 1000 to 10,000 AU, both of which are small enough so neutral atoms must be moving together with, and have the same temperature as the interstellar plasma in the local fluff. The neutral beam velocity vector gives us the plasma velocity vector. This forces the conclusion that there is an interstellar wind blowing on the heliosphere in the ecliptic plane, at a speed, VI = U = 25 km/s. The plasma density is < 0.3 per cubic centimeter and its temperature is ~ 7000 K. The existence of this wind is the reason the stagnation point flow shown in Figure 2 is accepted as the most likely configuration for the heliosphere.
OUR PRESENT UNDERSTANDING OF THE HELIOSPHERE
Guided by Table 1, the fast mode speed, cf, in the local fluff may be between 10 and 40 km/s (the sound speed is 10 km/s). Thus, VI may be larger than cf which would modify the configuration shown in Figure 2 in three ways. First, a bow shock can form, much like the bow shock in front of the Earth`s magnetosphere. Second, if VI is supersonic, the pressure on the downstream side and flanks of the termination shock is reduced, causing the shock to be further from the Sun in these directions. These two effects have been numerically modeled in a few cases, an example of which is shown in Figure 3 in which VI is assumed to be highly supersonic (The empty circle inside the termination shock represents the inner boundary for the calculation and has no physical significance.). Thirdly, since BI will generally not be aligned with the heliotail, the configuration will no longer be axisymmetric about the heliotail axis. However, effects of an arbitrary BI have not yet been incorporated into numerical simulations.
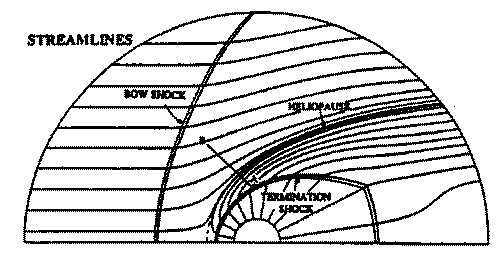
There are many things that have still been ignored in models. For example, the solar wind dynamic pressure depends both on time and on position. It is likely that the termination shock will consequently move inward and outward over the solar cycle by many AU, and by a few AU over times as short as one month. Thus, during encounters with the shock by Voyages 1 and 2 the shock may move back and forth over the spacecraft several times once the shock is first encountered. Also ignored are the magnetic fields in the solar wind and the interstellar medium. Both magnetic fields will modify the shape and position of the heliopause and these fields control the access and motion of galactic cosmic rays into the heliosphere. With regard to shape of the shock, if the interstellar field is large enough so that VI < cf, the fast mode speed, then it is expected that the shock and heliopause will be more like the configuration shown in Figure 2. In this case, Pioneer 10, which is farther out than Voyagers 1 and 2, but is travelling more slowly in the downstream direction, may be the first spacecraft to reach the shock.
DISTANCE TO THE TERMINATION SHOCK
The distances to the termination shock and to the heliopause are not known. Still, with equation (1) and more sophisticated derivative calculations, it is possible to make estimates. Figure 4 shows such a calculation of the shock distance in the upstream direction for a range of interstellar field strengths and densities. The estimated values for R range between 60 and 150 AU for the parameters from Table 1. This now forces the question of whether there a way of remotely determining R. This influences whether we will continue to collect data from spacecraft in the outer heliosphere. If Pioneer 10 and Voyagers 1/2 have any possibility of passing the shock and the heliopause, it would be a great addition to our knowledge of the heliosphere. Only a finite time exists because Pioneer 10 has about reached its limits and the Voyagers will run out of electrical power by about 2030.
There have, in fact, been several tentative remote detections of the termination shock and heliopause Of these, probably the most tantalizing is the detection of radio emissions coming from the outer heliosphere. It is hypothesized that the emissions are coming from the nose of the heliopause - the stagnation point, and that the distance to the stagnation point is somewhere between 116 and 177 AU. These distances place R between 60 and 160 AU, which is reachable by the Voyager spacecraft. There are also suggestions of a small value for R from cosmic ray modulation over the solar cycle, but this is highly tentative because we still do not have a good understanding of galactic cosmic ray access to and propagation in the heliosphere.
To summarize, the heliosphere is probably well represented as stagnation point flow occuring between the solar wind and an interstellar wind. The resulting configuration is similar to the Earth's magnetosphere. Inside the heliopause, the solar wind passes through a termination shock that is elongated in the downstream direction and which is moving back and forth at speeds up to 100 km/s. The presence of three spacecraft in the outer heliosphere is a unique opportunity to explore the structure and properties of the termination shock, heliosheath, heliopause, and VLISM. This opportunity is realizable based on the indirect evidence we have that R is probably ~ 100, and may be as small as 60-70 AU.
Axford, W. I., The interaction of the solar wind with the interstellar medium, Solar Wind, NASA SP-308 (C. P. Sonett, P. J. Coleman, Jr., and J. M. Wilcox, eds.), pp 609-657, NASA, Washington D.C., 1972.
Baranov, V. B., Gas dynamics of the solar wind interaction with the interstellar medum, Space Sci. Rev., 52, 90-120, 1990.
Grzedzielski, S., and D. E. Page (eds.), Physics of the Outer Heliosphere, COSPAR Colloq. Series V. 1, Pergamon Press, Oxford, 1990.
Holzer, T. E., Interaction between the solar wind and the interstellar medium, Ann. Rev. Astron. Astrophys., 27, 199-234, 1989.
Parker, E. N., Interplanetary Dynamical Processes, Interscience, New York, 1963.
Suess, S. T., The heliopause, Reviews of Geophysics, 28, 1, 97-115, 1990.