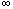Acknowledgments: Work reported herein has been supported, in part, by MIT's Total Data Quality Management (TDQM) Research Program, MIT's International Financial Services Research Center (IFSRC), Fujitsu Personal Systems, Inc., Bull-HN, and Advanced Research Projects Agency and USAF/Rome Laboratory under USAF Contract, F30602-93-C-0160.

ABSTRACT: The use of information systems in organizations is restricted by the quality of the data that appears in these systems. Correctness, completeness, precision, timeliness, and usability are defined as important dimensions in the assessment of the level of data quality that exists. Three approaches to incorporating and improving data quality are identified: 1) building semantically rich data models; 2) reinforcing databases with a large number of database constraints; and 3) restricting the use of data to predefined processes. Each of these is discussed and illustrated. Building upon this work, future research will investigate and demonstrate how to take advantage of these approaches for improving the quality of organizational databases.

Formal models using statistical and mathematical analysis depend critically on organizational data. The quality of the data used by these formal methods is an important issue for organizations that rely on data analysis for decision making. Managers traditionally receive training in statistical and mathematical analysis of data to achieve a high level of competence in the use of these formal methods; however, the quality of the data, is often merely assumed. Although formal method have been used to control data quality (e.g. [Liepins & Uppuluri, 1990] ), there is still considerable evidence that the quality of organizational data may often be quite poor, and may be a major source of errors and losses [Johnson, Leitch, & Neter, 1981] .

Many approaches, both organizational and technical, can be used to improve the quality of data. In this research, we address the data quality problem from the system's perspective. In general, there are three primary approaches to building systems that would improve the quality of data: l) building semantically rich data models; 2) reinforcing databases with a large number of database constraints; and 3) restricting the use of data to predefined processes.

The quality of data in a conventional database management system has been treated implicitly through functions such as recovery, concurrency, integrity, and security control. Although these functions are necessary, they are not sufficient to ensure data quality [Wang, Reddy, & Gupta, 1993] . This research investigates how the three above approaches can be used to improve data quality.

This extended abstract is divided into five sections. Section 2 identifies some major data quality dimensions. The three system solution approaches to data quality problems are outlined in Section 3 and examples illustrating the approaches given in Section 4. Section 5 summarizes and concludes the paper.

The first step to improving data quality is understanding the dimensions of data quality and their relative importance. Although correctness and completeness of data, intuitively, are very important, there are a number of other characteristics of data quality that need to be considered [Ballou & Pazer, 1985; Wang, Storey, & Firth, 1993; Wand & Wang, 1994] . Among them are precision, timeliness, and usability. and the purposes of this research, the following working definitions are used.

1. Correctness is defined as the "data item captured in an information system reflects the real-world state it is intended to represent"[Wand & Wang, 1994] .

2. Completeness occurs "when all values for a certain variable are recorded" [Ballou & Pazer, 1985] . Wand and Wang [1994] , in contrast, define completeness as when "all the real world states that one wishes to model are captured in the representing information system."

3. Precision is identified by Wand and Wang [1994] as a special case of ambiguity. They define ambiguity as multiple real-world states being mapped to a single information system state. For example, if there is an insufficient number of digits in an information system to represent multiple real-world states, then the user would not be able to interpret how a data item in the representing information system maps to the original real-world state that the data item is meant to represent.

When an actual value (real-world state) is not known (e.g., forecasting salaries for future years), multiple information system states may be used to represent the actual value. This can also be classified as a precision problem without ambiguity. In contrast, it may not be easy to record an actual value exactly (e.g., the exact amount of inventory quantity on hand). Under such circumstances, a data item in the representing information system may reflect an incorrect, as opposed to imprecise, real-world state. Clearly, some applications are more tolerant than others with respect to precision.

4. Timeliness is defined as "the recorded value is not out of date" [Ballou & Pazer, 1985] . Timeliness has two components, currency and volatility. Currency reflects the age of data, whereas volatility reflects the rate at which the data becomes obsolete. For example, George Washington's birthday may come from a 100-year old source that is not current, but is still timely because there is no volatility. On the other hand, stock market data could be from a source that is two minutes old which is very current, but because of its volatility, it is may not be timely for trading purposes.

5. The usability of data measures the usefulness of that data for a particular application at hand. The usability of data is relative to the processing needs of an application with some applications needing more highly processed data than others.

Three major approaches to building systems to improve the quality of data are outlined below.

1. Build semantically rich data models that capture more data semantics. These models would: (a) disallow data that do not have correct semantics; (b) require the acquisition of missing data to ensure completeness; and (c) quantify and record the quality of the data within the data model. These models require that data quality dimensions be included at the conceptual design stage (e.g. [Tu & Wang, 1993] ).

2. Reinforce databases with a large number of constraints [Orman, 1993] to identify and reject problem data, and link the data to appropriate applications in terms of data quality dimensions.

3. Restrict the use of data to predefined processes in order to eliminate the misuse of data. This might be done by encapsulating the data with their appropriate applications as is found in object oriented systems [Kim & Lochovsky, 1989] .

Each approach has its strengths and weaknesses. In a semantic data model, data must be maintained independently of their applications. As a result, the precision, timeliness, and usability of the data must be quantified and recorded using objective, application-independent measures.

In the object-oriented approach, data may be acquired and maintained in a manner that is most appropriate for each application. However, applications with diverse needs for precision, timeliness and usability cannot be supported by the same nonredundant database. Similarly, correctness and completeness must be maintained by the individual applications.

The constraint based approach is a compromise between the two. Using constraints, the interaction between the data and the applications can be recorded independently of both the data and the applications as can the match and the mismatch between the data quality and the quality needs of an application.

In this section, an example is provided for each data quality dimension, which is used to analyze the effectiveness of the three system's approaches. Then the interaction among the various dimensions is illustrated.

4. 1 Examples

4 .1.1 Correctness

Assume an employee database exists which contains the following entities and attributes:

EMPLOYEE: [Name, department, salary]

DEPARTMENT: [Name, manager]

Correctness can only be maintained with respect to preestablished semantic rules. For example, assume that salaries can not exceed 90I~, and managers always earn more than their employees. Any data that violates these rules is deemed incorrect. The three approaches deal with this correctness problem in different ways.

The semantic data model approach incorporates this information into the data model through domain definitions, and additional relationships to capture the violations. For example, a relationship "incorrect" could be defined between Employee and Manager to capture those pairs that violate the integrity.

The constraint approach expresses these rules in first order logic, and stores them separately from the data.

EMPLOYEE(x,y,z) 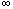z < 90K

EMPLOYEE(x,y,z) AND DEPARTMENT(y,w) AND EMPLOYEE(w,y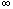,v) z<v

These rules are very general since they have the power of first order logic. The disadvantage of this approach is the efficiency of managing a large number of constraints. The storage, retrieval, and efficient execution of the constraints is a critical concern. An efficient methodology to store constraints as sample data has been proposed [Orman, 1993] . A variety of methods to improve the execution efficiency of constraints have been suggested. They vary from substitution of update constants into constraints before execution [Berstein & Blaustein, 1981; Nicholas, 1982] to theorem proving techniques [McCune & Henschen, 1989; Orman, 1995] .

The encapsulation approach has been used extensively in object oriented programming. It involves encapsulating data with the processes that uses it, with each capsule responsible for the quality of its own data. This approach is effective with data that is private to a small number of processes, but large shared organizational data bases still have to be maintained using a different approach. Consider the employee database above, and two processes HIRE and GIVE RAISE. Each process will modify the salary data, and hence must be responsible for the maintenance of its correctness as of the time of creation or modification. The salary data, for example, can be duplicated and stored with each process separately, and with each process maintaining its own data quality. When a raise is given, the process makes sure that it does not exceed the salary of the appropriate manager. Alternatively, a shared depository can be employed to maintain quality for both processes using one of the other methods.

4.1.2 Completeness

Completeness is established with respect to preestablished requirements of the existence of data. Given the same database, assume that each department is required to have at least two managers, and each employee is required to have a salary.

The semantic data model approach would extend the data model to incorporate a count of the minimum number of managers of each department. The constraint approach is similar to the previous case:

EMPLOYEE(x,y,z) 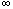z null

DEPARTMENT(x,y) DEPARTMENT(x,F(x,y)) AND F(x,y) y

(where F(x,y) stands for a second manager for department x is different from y.)

The encapsulation approach requires the application to check whether a data item exists before execution; that is, to check for the existence of at least two managers for each department .

4. 1.3 Precision

For data items, such as forecasted salaries for future years, the precision of data can be expressed as a probability distribution of the actual value around the value stored in the database. They would be stored with a range or with an actual probability distribution around a stored value. This would be the approach taken by semantic data models since the storage is independent of the applications. The constraint and encapsulation approaches require that the precision needs of an application be represented as well as possible matches between the data and the applications.

4.1.4 Timeliness

In general, timeliness is a function of currency and volatility. Wang, Reddy and Gupta [1993] propose that, letting C represent currency with a value between 0 and 1 (0 indicates a data item has just been created or updated), and V represent volatility with a value between 0 and 1 (where 0 means no change), then, timeliness can be computed as T = 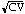, where T is between 0 and 1 (0 is the best and 1 is the worst).

In the semantic data model approach these parameters are incorporated directly into the model, and the applications use these parameters in evaluating the appropriateness of each data item for their purposes. The disadvantage of this approach is the requirement to have one set of parameters for all applications using the same data. In fact, the volatility measure appropriate for each application may be different. Volatility of stock prices may very well depend on the application; for example, a trader may have a different volatility measure than a market analyst or a university researcher.

The constraint approach provides more flexibility by matching applications with data that meet the timeliness requirements.

The encapsulation approach goes a step further and maintains separate data with each application whenever their application's timeliness requirements vary. Consider an inventory control system that is used both for replenishing inventory, and for responding to customer requests. The two applications may have different measures of volatility for their inventory values. The customer requests application may require up to the minute information about inventory to determine if the request could be supplied, and hence the inventory values would be considered highly volatile. The reorder system on the other hand may have some slack if the cost of running out of stock is not very high, as long as the customer can be provided with a good estimate of when to expect the product. In this case the inventory values may not be considered volatile. Then, some degree of duplication may be appropriate if no common measure of timeliness can be found.

4. 1.5 Usability

Usability refers to the processing required before the data is appropriate for the application. Consider an application that requires the average salary per department. This information is not immediately available from the database, but requires some processing. Semantic data models can define such derived data items within the data model, but it is usually not advisable since the semantics of derived data are often complex and vary from application to application. Constraints are slightly more effective in expressing derived data in terms of raw data, and using these rules to guide the derivation. Encapsulation is the most effective in maintaining derived data, since derived data can be bundled with the processes that use them, and the decision whether to also store the raw data redundantly can be made within the process.

4.2 Interaction of Dimensions

Data quality dimensions may interact. The following example illustrates some of the issues that arise when they do so. Consider a retailer who stores scanner data in addition to inventory data. Two typical entities in this application, along with their attributes are:

SALE: [Item, quantity]

INVENTORY: [Item, price, quantity-on-hand]

The SALE information is received directly from the point of sale scanner. The inventory is created by the stock takers, and updated periodically using the SALE information. This example is useful in demonstrating various data quality dimensions since it contains both observed and derived data, and different methods of observation are likely to involve different sources of error. The following constraints can be identified:

One can not sell more than the quantity on hand.

SALE(x,y), INVENTORY(x,z,w) y²w

No sale should cost more than 1000 dollars; otherwise a manager's approval is needed.

SALE(x,y), INVENTORY(x,z,w), yz=t t²$1000.00

Several important issues should be noted. First, the correctness of the quantity on hand of a data item depends on how often a file is updated (timeliness). Second, are all sales being captured at the scanner (completeness)? How is the scanner data represented (precision)? If the quantity on hand is not exact (precision or correctness), then should every transaction that exceeds the quantity on hand be rejected (usability)? An error would occur only if the difference is more than some specific value that measures the correctness of the quantity on hand. This correctness, in turn, is a function of how long ago the INVENTORY file was updated (timeliness).

In this extended abstract, we have provided working definitions for five major dimensions of data quality, and identified three systems approaches to improving these data quality dimensions. Each of the dimensions was analyzed in terms of these system approaches and illustrated through examples. In addition, an example of how these dimensions may interact was presented. Future research will investigate and demonstrate how to take advantage of these approaches for improving the quality of organizational databases. This entails the development of a semantic data model at the conceptual level, with an object oriented implementation that includes a constraint facility. Case studies in different industrial settings will also be conducted to validate the conditions under which each of these three approaches will be most effective.

[1] Ballou, D. P. & Pazer, H. L. (1985). Modeling Data and Process Quality in Multi-input, Multi-output Information Systems. Management Science, 31(2), 150-162.

[2] Berstein, P. A. & Blaustein, B. (1981). A Simplified Algorithm for Integrity Assertions and Concrete Views. Proceedings of COMPSAC, .

[3] Johnson, J. R., Leitch, R. A., & Neter, J. (1981). Characteristics of Errors in Accounts Receivable and Inventory Audits. Accounting Review, 56(2), 270-293.

[4] Kim, W. & Lochovsky, F. (1989). Object-Oriented Concepts, Databases, and Applications. New York: ACM Press.

[5] Liepins, G. E. & Uppuluri, V. R. R. (Ed.). (1990). Data Quality Control: Theory and Pragmatics. New York: Marcel Dekker, Inc.

[6] McCune, W. W. & Henschen, L. J. (1989). Maintaining State Constraints in Relational Databases. Acta Information, 18(1), 46-48.

[7] Nicholas, J. M. (1982). Logic for Improving Integrity Checking in Relational Databases. Acta Information, 18, 227-253.

[8] Orman, L. (1993). Constraint by Example. Proceedings of Third Annual Workshop on Information Technologies and Systems (WITS), (pp. 40-47) Orlando, Florida.

[9] Orman, L. (1995). Databases Constraints as Counterexamples. Acta Information.

[10] Tu, S. & Wang, R. Y. (1993). Modeling Data Quality and Context through Extension of the ER Model. A. Hevner & N. Kamel (Ed.), Proceedings of Third Annual Workshop on Information Technologies and Systems (WITS-93), (pp. 40-47) Orlando, Florida.

[11] Wand, Y. & Wang, R. Y. (1994). Anchoring Data Quality and Context through Extension of the ER Model. (No. TDQM-94-03). MIT Sloan School of Management.

[12] Wang, R. Y., Reddy, M. P., & Gupta, A. (1993). An Object-Oriented Implementation of Quality Data Products. A. Hevner & N. Kamel (Ed.), Proceedings of Third Annual Workshop on Information Technologies and Systems (WITS-93), (pp. 48-56) Orlando, Florida.

[13] Wang, R. Y., Storey, V. C., & Firth, C. (1993). Data Quality Research: A Framework, Survey, and Analysis. In Data Quality: A Critical Issue in the 1990's and Beyond. (pp. Orlando, Florida: Data Quality Panel of the third Workshop on Information Technologies and Systems (WITS-93).