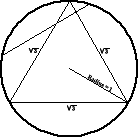
The Solution
Answer : 1/3
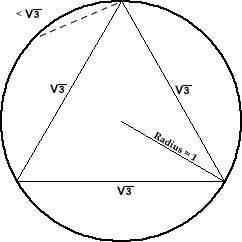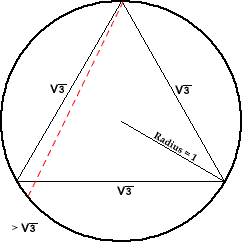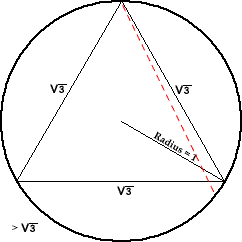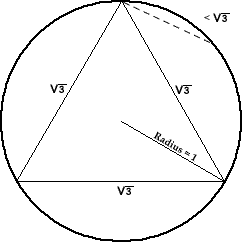
We generate the random chord by randomly choosing its end on the circle.
By symmetry, we can fix one of the ends. The moving end generates a chord with
a length greater than the square root of 3 when it's on the portion away from the fixed end, with length one third of the circle length.
So, the probability that the random chord has a length greater than the square root of 3 is 1/3.
Here is an animation that explains the way we can get to this answer:
back to the answers page
By symmetry, we can fix one of the ends. The moving end generates a chord with a length greater than the square root of 3 when it's on the portion away from the fixed end, with length one third of the circle length.
So, the probability that the random chord has a length greater than the square root of 3 is 1/3.
Here is an animation that explains the way we can get to this answer:
