3.1
(a) 268.8 K and 4.62510⁵ Pa
(b) at 90^o (horizontal) 282.6 K and 4.86310⁵ Pa
(c) at 180^o (vertical downward) 296.4 K and 5.110⁵ Pa
 

3.2
(a) Q/t = 3.5110⁸ J/hr [contractor pays]
(b) Q/t = 3.2310⁸ J/hr [contractor collects fee]
 

3.5
(a) L_A = 0.4352 m, L_B = 0.0218 m, T_A = T_B = 311 K, P_A = P_B = 7 bar
(b) Same as (a)
(c) There is no real solution given the constraints, we must specify more about the expansion (or compression) of A or B. For example, if A expands adiabatically, P_A = P_B = 6.68 bar, T_A = 263.6 K, T_B = 881.3 K, L_A = 0.3917 m, and L_B = 0.0655 m.
 

3.12
(a) After 6 s, T = 349.5 K, P = 1.13910⁵ Pa in the bulge.
(b) After 3 s, T = 454.6 K, P = 6.2610³ Pa in the large tank.

4.1
For the minimum condition T_A(final) = 132 K and for the maximum condition T_A(final) =617 K, these extrema require using the object with the lowest mass x heat capacity product.
 

4.2
W = 9.807y in J/kg evaporated, for typical values of ambient dry bulb and wet bulb temperatures of 300 K and 280 K respectively, y = 16.8 km!
 

4.3
(a) _B = 0.166 mol/s,-_C = 0.833 mol/s
(b) T_D = 299.1K
(c) W = -26.4 J/s
(d) S= 13.3 J/K
(e) Same as (d).
(f) = -4000 J/s
 

4.4 W = - 1.1110⁴ J, T_f = 288.7 K, P_f = 0.54 bar
 

4.6
(a) 21.6 s
(b) 391.8 K and 2.2 bar at 10 s
(c) S_gas= 4.9310³ J/K = S_universe
(d) S(gas in tank) = -813.6 J/K,
-----S(gas vented) = +2020 J/K,
-----S(surroundings) = +1203 J/K
(e) W_min = +2.8310⁵ J
 

4.7
(a) = 2400 W, T = 327.7 K, and Q = 22,200 J after 10 s
(b) T = 1750 K at t = 57.7 s with all stored work consumed.
 

4.9
(a) W_net = - 3.1710⁶ J
 

4.12
(a) T₂ = 227.9 K, T₁ = 392.9 K (2) after venting (1) before venting
(b) T₂ = 211.1 K, T₁= 363.9 K
(c) W = 2547 J/mol
(d) W_max = 1.3810⁵ J/kg
 

4.13
(a) S = -1.3810³ J/K hr
(b) S = 2 J/K hr
 

4.16
(a) Case (1) 1.9810^-2 kWhr; (2) 2.7810^-2 kWhr; (3) 2.1610^-2 kWhr; (4) 2.7810^-2 kWhr
(b) Case (1) 420 K, 42 J/K; (2) 300 K, 0 J/K; (3) 300 K, 73.9 J/K; (4) 300 K, 0 J/K
 

4.18 W = 5.2310³ J = -Q

4.22
(a) P = 6.3510⁴ Pa
(b) T = 272.8 K
(c) P = 3.6810⁴ Pa with 2 pumps
(d) P = 1.9110⁴ Pa and T
(e) Power (minimum) = 20.9 W
 

4.24
(a) W_max= -198.76 kJ/kg (Carnot + expansion work)
(b) W_p = ideal pump work (estimated to include PE for lifting water and for the compression of gas space in storage tanks)
 

4.30
(a)  = 6.3810⁶ J/s
(b)= 0.90 = (actual power)/(maximum power)
(c) no, the maximum power outputs are the same

5.2
(a)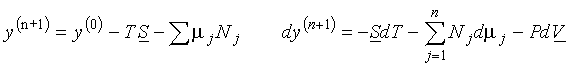 
(b)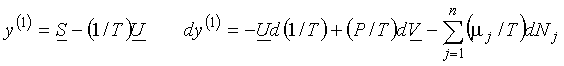 

5.4
(a) 
(b) 
(c) U
(d) 
 

5.7
(a) 
(b) 
 

5.10 T_f = 1087 K
 

5.12 
 

5.21 V_c = RT = (C_p/C_v) RT » 330 m/s (use mass units for R with molecular weight) distance at 2 s » 660 m
 

5.22
(a) 
 

5.23
(b) No, the ratio as shown in Problem 5.17 is expressed in terms of PVT properties and an isentropic derivative which in turn requires non-PVT property information specifically related to the temperature dependence of energy stored in U.
 
 

5.24
(a) 
(b) 
(c) 
(d)
(e) 
 

5.25
(a) 
(b)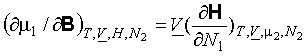 
(c) Yes, using the Gibbs-Duhem relationship:

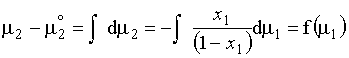
6.2

thus,  at equilibrium
 

6.3
- from chemical equilibrium criteria, intersections define equilibrium states.
 

6.4
(a) 
----
-----
-----
 

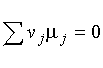
6.5
(a), 
(b) T = 366.5 K, P_A,1 = P_A,2 = 2 bar, P_B,2 = 1 bar
      N_B,1 = 0 N_B,2 = 1 mole N_A,1 + N_A,2 = 4 moles
(c) P₁ = 2 bar, N₁ = 5 moles; V₁ = 2.5 RT/10⁵ = 0.0752 m³ with T = 367 K and no gas on side 2.
 

6.7
Fraction evaporated 0.227

7.1
if A_NN = 0 then A_VV = 0 = A_NN /V ²
 

7.3
T = 55.1 K
 

7.6
for  = 2.5
 

xA	xB
0.1	0.286, 0.614
0.2	0.4 (critical pt.)
0.3	no solution
0.4	0.2, 0.4 (critical pts.)
0.5	0.175, 0.325
0.6	0.085, 0.28

7.11

8.4
At 365.8 K, 16.5 bar

 

8.5
At T = 319.4 K
 

Pr	KH/KS	Z = PV/RT
0.1	0.100	0.967
0.2	0.194	0.932
0.4	0.369	0.862
1.0	0.798	0.598
4.0	0.426	0.547
10.0	-0.296	1.108

 

8.9
Using an isenthalpic expansion across an insulated value to 1 bar, 0.236 kg of dry ice could
be produced per kg of CO₂ drawn from the cylinder.  For an isentropic expansion, 0.41 kg dry ice/kg of CO₂ is possible.
 
 

8.10
(a) T_f = 379.3 K at 48.3 bar
(b) W = - 9.110⁷ J
 
 

8.14
T_B,f|256 to 257 K, P_B,f|21.5 bar, x_g = 0.63 (fraction vapor)
 
 

8.15
(a) Power = 508 kW
(b) Power = 516 kW
 
 

8.30
- = 90.9 kW and- = 68.3 kW
 
 

8.31

Yes, the vdW EOS gives at the Zeno condition (Z = 1) a straight line: T_r = T/T_c = 27/8 - (9/8) _r

9.1
(a) -31.36 kJ/mole water added to acid at the start; -61.1 kJ/mole and added to water
at the start
(b) maximum heat load occurs at the start
(c) total Q = - 28 kJ/mol acid = -11.2 kJ/mol of solution same for both cases
 

9.2
(b) Q = - 3.86 10⁵ J
(c)

(d)
 

9.3
mole % NH₃ = 51.37 %
 

9.6
W = 326 J
 

9.7

w = water and s = salt (NaCl)
 

9.8
(a) W_min = -1069 J (PREOS)
(b) W_min = -1812 J (ideal gas mixture)
 

9.9

 

9.11
 

x salt (wt fraction)
0.01	7.2	8.5
0.05	42.2	43.9
0.10	90.5	91.1
0.15	156.6	142.0
0.20	242.0	197.0
0.25	355.0	257.0

9.13


 

9.14
(a) 
(b) At -85^oC (188 K), there are two phases in equilibrium at x_EtOH = 0.07 and 0.35.
 

9.20
= 675 W

 

9.21
(a) 1.3210⁵ W
(b) See Section 14.4 for details, information provided in part (a) is not sufficient, ideal gas state heat capacities and a mixture PVTN EOS are needed.
 

9.27

10.2
H - H^o = PV - RT - a/V
 

10.3




 

10.4

10.6 



 

10.7
b = 
a = 
 

10.9
(a) 
(b) 
(c) for T/T_c = 1.00001,

 

10.10

11.4
(a) 
(b)
(c) for only positive values of , a large number of values 
exist as a function of x_i that yield extrema, e.g.
for x₁ = 0.2
 
 

0	3.236
0.500	1.699
1.000	1.000
1.500	0.586
2.000	0.209
2.118	0

 

11.5
for 
for 
 

11.7
(c) fraction of solution precipitated = 0.0067
 

11.8
for 2-suffix Margules T_c = w/2 k
 

11.9
for quasi-chemical model T_c = w/2.23 k

12.3
(a) selected values of are given below for LiCl
 

molality	-(Meissner)	-(Pitzer)
0.1	0.9651	0.9653
0.01	0.9032	0.9044
0.1	0.7850	0.7927
1.0	0.7636	0.7758
5.0	1.9586	2.0222
10.0	7.9948	11.0827

(b) 
given that s = 9 mol/kg for pure LiCl in H₂O. Using the Meissner model for  predictions for both pure and mixed electrolyte.
        K_sp(9)² (~6)² = 2916 for pure LiCl at 25^oC

        Iterating s*=2.4 and  3H for mixed LiCl and HCl at 25^oC
(c) Difficult to say without more information on how much Na₂SO₄ influences for LiCl.  For example is the effect on  large enough to compensate for the Cl^- common ion effect?
 

12.8
Some representative values for 

molality (NaCl or LiCl)(CuCl2)
0.1                                 0.96                                         0.55
1.0                                 0.30                                         0.18
10.0                               0.096                                       0.055

At T = 300 ^oC 22.3 so multiply above values by (22.3 573)/(78.5)(298) = 0.74
 

12.10
I = 0.546 or m = I / 3 = 0.182 molal

13.2
Using Joback’s method with T_b = 225.5K (exp. value)
 -T_c = 364 K, P_c = 46.7 bar, and = 0.1606
- = -2.83 + 0.269 T = 3.1510^-4 T ² + 4.210^-8 T ³
 

13.3
T_c = 663.5 K, P_c = 32.21 bar, V_c = 429.5 cm³/mol, and T_b = 450.38 K
Using Eq. (13-18) for vapor pressure:

 

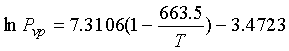
13.4
For pure caffeine, T_b640 K, T_c = 872 K, V_c = 488.5 cm³/mol, and P_c = 41.46 bar
Using the PR EOS for density estimate for 5 mol % caffeine CO₂ mixture at 80 bar, 310 K = 1151 kg/m³. The vapor pressure of liquid caffeine is approximated by Eq. (13-18)

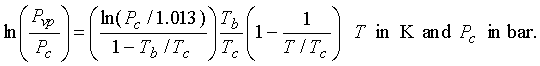
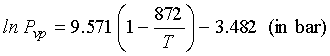
14.2
Using the PR EOS,




 

14.6
(a) 
(b) 
(c) Using the RKEOS and a suitable mixing rule, a_mix and b_mix parameters can be calculated and used to calculate all PVTN properties. With an ideal-gas state C_p all derived properties needed for the cycle calculation can be obtained using a departure function approach. Then,

 

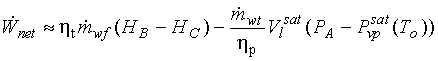
14.8
(a)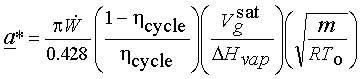 
(b)  (about 150 times smaller!)
 

14.12
(a) and (b) 
      so CTI’s claim of 1 kWhr production violates the 2^nd Law limit
(c) All heat transfer and work production and utilization steps have some irreversibility in practical systems.
 

14.14
(a) 
(b) no fundamental laws or concepts are violated
(c)  about 17% more area for heat exchange is required for the GH process
(d) 

NB: If an electric motor drive is used for the feed pump in the conventional Rankine system, then the net output would be reduced possibly accounting for the discrepancy.

15.1

 

15.3
x (Naphthalene) = 0.196
 

15.6
(c) q (critical quality) = 
(e) O₂: q = 0.54 and H₂: q = 0.36
 

15.12
x_KCl = 0.413 and T = 624 K
 

15.13

 
 

15.15
Anesthetic pressure of CCl₄- 4.910^-3 bar.
 
 

15.19
(a) 
(b) 
(c)
     (i) , solution is regular
     (ii), less structural ordering in mixture versus pure state
     (iii), more structural ordering in mixture versus pure state, implies 

16.9
(a) y_A = 0.764 y_B = 0.236
(b) not in equilibrium, estimate y_B assuming equilibrium
 

16.12

 

16.14

 

16.16
using expansion valve
using expansion turbine
Consider net energy, entropy, and work flows using 1^st and 2^nd Law concepts to show process is not feasible as described.
 

16.20
(a) P = 21.9 bar
(b) T = 51.5 K
(c) 
 

16.22
T, K       C_p (effective), J/gK
293                         4.69
313                         7.20
333                         8.29
353                         6.36
373                         3.64

17.3
(a) ; at A: L₁-L₂-H-G and at B: L₁-H-I-G
(b) L₁ = 0 and M₁ = 0 use P-explicit EOS to determine required A_ijk and A_ij derivatives
(c) 
(d) 
_{in this case}
 

17.6
d ln P/d(1/T) = 

18.1

 

18.4
_{J/kg mol}
 

18.5
T_i = 269 K = -4^oC (winter!)
 

18.6
T_bath = 317 K, efficiency = 0.065
 
 

18.8
z = depth = 764 m
 

18.9
(tube bottom) = 0.501, if L  4/7
 

18.11

 
 

18.14
y_tritium = 0.065 and y_deuterium = 0.538 at rim
 

18.16
h = 252 m, for equilibrium ocean, fresh water cannot rise above a level 252 m below sea surface. For the well-mixed case, process becomes feasible if Z = depth > 9850 m (32,000 ft.).

19.1

 

19.2

 

19.5

 

19.7
x_butanol = 0.436
 

19.8
(a) 0.046 J/m²
(b) 296 K