Understanding how biological systems process and respond to environmental cues requires the simultaneous examination of many different species in a multivariate fashion. High-throughput data collection methods offer a great deal of promise in offering this type of multivariate data, however, analyzing these high-dimensional datasets to identify which of the measured species are most important in mediating particular outcomes is still a challenging task. Additionally, when designing subsequent experiments, existing datasets may be useful in selecting the measurements, conditions, and time points that best capture the relevant aspects of the full set.
Information theory offers a framework for identifying the most informative subsets of existing datasets, but the application to biological systems can be difficult when dealing with relatively few data samples. The goal of this project is to develop and validate a method for approximating high-order information theoretic statistics using associated low-order statistics that can be more reliably estimated from the data. Using this technique, we aim to identify subsets of biological datasets that are maximally informative of the full system behavior or of defined outputs according to information theoretic metrics.
Information theory provides a natural framework for identifying sets of features that have signicant statistical relationships with each other or with external variables. The two fundamental concepts from the theory are information entropy and mutual information (MI) which quantify statistical uncertainty and statistical dependency, respectively. Though similar to the correlation-based statistics variance and covariance, the information theoretic statistics have important advantages. In addition to being invariant to reversible transformation and able to capture nonlinear relationships, information theoretic statistics can be applied to categorical variables (such as the classification of a particular tumor) as well as continuous ones (such as the expression level of a gene from a microarray). These statistics can also be extended to quantify the relationships of sets of features using joint entropy and multi-information.
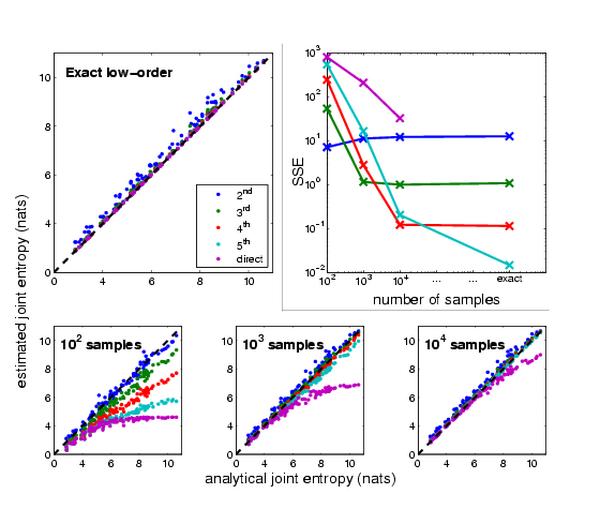
At the core of the project is a method for approximating high-order information theoretic statistics such as information entropy and mutual information from associated low-order terms. Estimating high-order entropies directly from sparsely-sampled data is extremely unreliable, while estimating second- or third-order entropies reliably has been shown to be possible. In many biological systems, high-order interactions may be rare, meaning that a model incorporating only low-order information can often perform reasonably well.
To assess the performance of the various levels of approximations in different sampling regimes, we explored a series of randomly generated relational networks with analytically computable entropies with widely varying topologies and orders of influence. Using our approximation framework, we have shown that for the sampling regimes typical of biological systems, the low-order approximations significantly outperform direct estimation.
We aim to apply these approximation techniques to identify subsets of high-dimensional biological datasets that are most informative of system outputs. We have begun projects involving a variety of types of data and for a range of applications including:
