


1.4 NEED FOR A PROBABILISTIC ANALYSISMost urban services face uncertainties related to time of occurrence, type, location, and quantity of demands. Considering an individual household, for instance, the amount of refuse it generates, the amount of mail it sends and receives, its need for emergency assistance (from police, fire, ambulance, or emergency repair services), and its use of public and private transit facilities fluctuate from day to day. True, there are regular statistical patterns that allow us to predict reliably the percentage of transit riders that will use a system between, say, 5:00 and 6:00 P.m., or the fraction of a city's refuse that will be generated from a particular neighborhood over the course of a year. But the exact time and location of any particular demand for service, unlike scheduled arrivals at a doctor's office, cannot be predicted. Such uncertainties can cause system congestion even when, on the average, there is sufficient system capacity to handle demands. The need for a probabilistic analysis can be illustrated by a simple
example. Suppose that calls for emergency ambulance service are
generated from within a community at an average rate of one per hour.
For simplicity, we assume that all calls are serviced by the city's
single ambulance, which is stationed at the city's hospital. Any calls
that occur while the ambulance is busy on a previous call are entered
into a queue that is depleted in a firstcome, first-served manner. In
addition, let us assume that the average time to service each call
(i.e., the travel time to the scene, on-scene service time, travel time
back to the hospital) is 1/2 hour and the standard deviation is
Now, deterministic reasoning, which is not uncommon in present planning procedures, argues that this ambulance is not overloaded because it is busy on ambulance runs only 4 hours out of each 8-hour tour of duty. After all, the unit is being utilized at only one-half "capacity." The same reasoning argues that since the ambulance services calls twice as fast as they arrive, any queueing delay incurred by arriving calls should be negligibly small. Finally, using deterministic arguments, one should expect the number of calls generated during any 8-hour tour to be very close to the average, eight. Switching to probabilistic arguments, it has been found that the
generation of emergency calls in a city can be accurately modeled by the
Poisson process, a random process to be reviewed in Chapter 2. The
Poisson process arises when specific postulates governing microscopic
system behavior are satisfied. Nearly all of those apply to urban
emergency services. Given the Poisson assumptions, the number of
ambulance calls that occur during any particular 8-hour tour is a random
variable with the Poisson probability mass function, 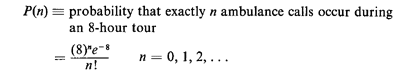
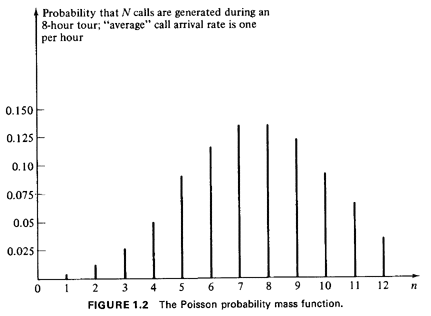
days. True, the average workload per tour, measured in hours required to service calls, is 4 hours. But one can show that there is considerable dispersion about this average, as measured by a standard deviation of 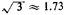 hours. Finally, using M/G/ I queueing theory (Chapter 4), one finds that
fully 50 percent of the calls arrive while the ambulance is busy and
thus have to be stacked in the queue; the average time spent in the
queue by these calls is 45 minutes, reflecting a truly congested system.
These insights illustrate the usefulness of a probabilistic analysis.
hours. Finally, using M/G/ I queueing theory (Chapter 4), one finds that
fully 50 percent of the calls arrive while the ambulance is busy and
thus have to be stacked in the queue; the average time spent in the
queue by these calls is 45 minutes, reflecting a truly congested system.
These insights illustrate the usefulness of a probabilistic analysis.
To implement the results of a probabilistic analysis, it is necessary that operational objectives be stated in compatible terms. For instance, the following statements exhibit probabilistic points of view: "Allocate sufficiently many ambulances so that 85 percent of emergency calls for ambulances can be answered without queueing delay," or "so that the average travel time to ambulance calls is 5 minutes." Although such explicit target levels for performance may be difficult to state (see Chapter 8), operating systems reveal implicit decisions that could be quite unacceptable if made clear to an agency administrator. We are now ready to begin our tour of models and methods for the analysis of urban service systems. Given the central role of uncertainty in the operation of these systems, our first concern deals with the fundamentals of probabilistic modeling. |