


2.10.2 ExpectationGiven a continuous random variable X with pdf fx(x), the expectation or expected value of the function g(X) is 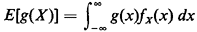
All the results concerning expected values derived in Section 2.7 carry over in the obvious way, with summations replaced by integrations. Exercise 2.13: Expected Values, Revisited Verify that the results of Exercises 2.6-2.9 also apply to continuously distributed random variables. Example 1: (continued) Here we continue our triangle problem initially described in Example 1, Section 2.1. We restate the problem as follows: "Two points X1 and X2 are marked randomly and independently on a stick of length 1 meter." a. Determine the probability that a triangle can be formed with the three pieces obtained by cutting the stick at the marked points. b. Determine the conditional pdf for X1, given that a triangle can be formed. C. Determine the conditional pdf for X2, given that X1 = 1/4 and a tri-angle cannot be formed. Solution: a. First we must interpret the word "random." In the absence of any further information, the most reasonable interpretation is that X1 and X2 are uniformly and independently distributed over [0, 1]. Thus, the joint pdf for (X1, X2) is 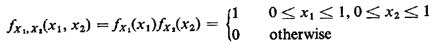
Letting 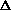 be the event that a triangle can be
formed, we recall that be the event that a triangle can be
formed, we recall that 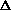 corresponds to the two triangular regions of the (X1, X2) sample space
shown in Figure 2.1. Since the area of each is 1/8 and since the joint
pdf is uniform with height 1, we obtain by inspection that P{ corresponds to the two triangular regions of the (X1, X2) sample space
shown in Figure 2.1. Since the area of each is 1/8 and since the joint
pdf is uniform with height 1, we obtain by inspection that P{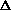 } = 1/4. If the pdf were not uniform, we would have to evaluate the following
integral: } = 1/4. If the pdf were not uniform, we would have to evaluate the following
integral: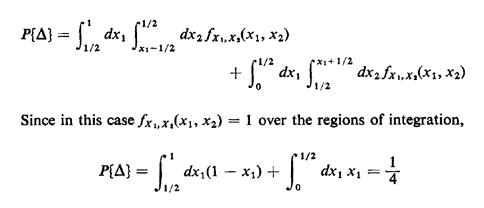
as we obtained by inspection. b. Given that a triangle can be formed, the conditional (X1, X2) sample space comprises the two triangular regions over which we have just integrated. If one invokes the definition of the marginal pdf in terms of probabilities of lying within infinitesimal strips, 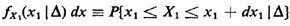
then one can see from Figure 2.1 that this "strip probability" increases linearly from 0 to a maximum at X1 = 1/2 and then decreases linearly (and symmetrically) back to zero. Thus, by inspection, 
as anticipated. c. The conditioning information is that X1 = 1/4 and a triangle cannot be formed. By inspection of Figure 2.1, the conditional pdf for X2 is 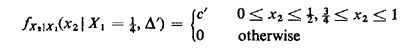
This pdf, which is displayed in Figure 2.10, is derived by considering a strip of infinitesimal width dx1 at x1 = 1/4. Integration requires that c' = 4/3. We could continue the process of conditioning indefinitely and, in theory, incur no additional problems. For instance, let A = event | X2 - 1/2 | > 1/8; this means that X2 is either less than 3/8 or greater than 5/8. Then 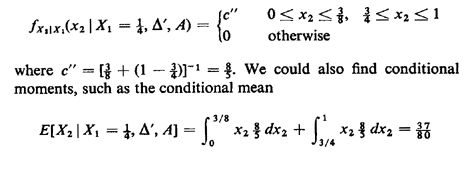

|