


2.10.4 The s-TransformFor continuous random variables the s-transform plays a role analogous to that played by the z-transform with discrete random variables. For a random variable X with pdf fx(x), the s-transform (or exponential transform or Laplace transform) is defined to be 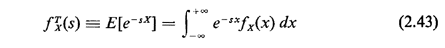
If s is considered to be a complex number, with real and imaginary parts, the integrals associated with s-transforms and their derivatives will be finite if the real part of s is zero. If P{X  a} = 0 for some finite a, these integrals will be finite
as long as the real part of s is nonnegative. In the remainder of
our work we will assume that the real part of s is chosen appropriately.
And again, as with z-transforms, emphasis in subsequent chapters will
not be given to transform techniques. a} = 0 for some finite a, these integrals will be finite
as long as the real part of s is nonnegative. In the remainder of
our work we will assume that the real part of s is chosen appropriately.
And again, as with z-transforms, emphasis in subsequent chapters will
not be given to transform techniques.Given the s-transform of a pdf, one can uniquely recover the pdf. In general, this is done by contour integration in the complex plane. For those s-transforms whose numerators and demoninators factor into products of terms (s - s1)(s - s2) . . ., the pdf can be recovered by partial fraction expansion. By direct substitution into the definition of the s-transform, one can verify the following moment-generating properties: 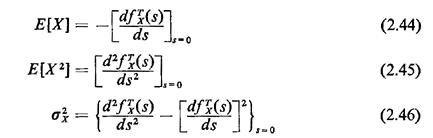
Applications of these relationships are shown in the following section. Exercise 2.14: s-Transform of a Sum Suppose that X1, X2, . . ., Xn. are mutually independent continuous random variables. Let R = X1 + X2 + . . . + Xn. Show that 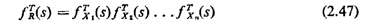
|