


2.11.2 Exponential PDFA random variable T is said to have an exponential pdf if 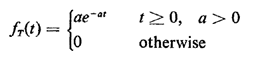
The mean, variance, and s-transform are 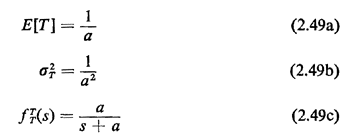
The exponential pdf arises in numerous contexts, including Poisson processes. It has a "no-memory" property similar to that of the geometric pmf. We demonstrate this in the following example. Example 4: Jitney Rider Suppose that a person walks to the side of the roadway to wait for a jitney, which will transport her to the next town. A jitney is a form of usually unscheduled transportation service involving minibuses or macro-taxicabs that travel back and forth between two towns or other centers. Jitney service, although uncommon in Europe and North America, is popular in many countries throughout the world. Suppose that, by analysis of past data or other means, it is known that the time required until the arrival of the next jitney is an exponentially distributed random variable with mean 10 minutes. Now suppose that our potential jitney rider has already waited 15.5 minutes and she wants to know the conditional mean additional time that she will have to wait. Solution: 
Hence, the conditional pdf is identical to the original exponential pdf but shifted to the right 15.5 units (Figure 2.11). By inspection, then, the conditional mean additional time that she has to wait remains 10 minutes. Here, 11 sunk investment" in waiting reaps no rewards in terms of reducing the remaining expected time until jitney arrival. 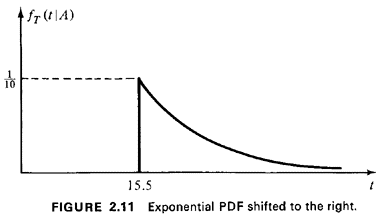
Exercise 2.15: Jitney Rider, Revisited Redo Example 4 assuming that the pdf for the time until arrival of the next jitney is uniform between 2 and 18 minutes. How does sunk investment affect waiting time in this case? |