


2.11.4 Gaussian PDFA random variable Y is said to have a Gaussian or normal pdf if 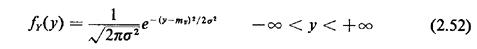
The mean, variance, and s-transforms are 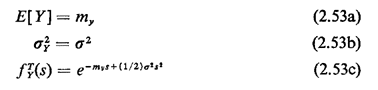
The Gaussian pdf arises most often in practice in applications of the Central Limit Theorem, which states (roughly) that the pdf of the sum of a large number of independent random variables approaches a Gaussian pdf with mean equal to the sum of the individual means and variance equal to the sum of the individual variances. The analyst of urban service systems should be familiar with this application of the Gaussian pdf. On occasion in this text we may invoke the Central Limit Theorem to approximate the pdf of a sum of random variables as a Gaussian random variable. Since we cannot obtain a closed-form expression for a partial integral of fy(y), tables of the Gaussian pdf and cdf are widely available, for instance in mathematics and engineering handbooks. |