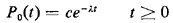2.12.1 Postulates of a Poisson Process
There are four postulates associated with the Poisson process: First
we state them informally, then mathematically:
| 1. | The probability that at
least one Poisson arrival occurs in a small time period t is "approximately" t is "approximately"  t. Here t. Here is called the
arrival-rate parameter of the process. In applications, a numerical
value for is called the
arrival-rate parameter of the process. In applications, a numerical
value for  is found by measurement. Examples
might be is found by measurement. Examples
might be = 10 fire alarms per hour, or = 10 fire alarms per hour, or  = 62 cars per hour passing through a tunnel, or = 62 cars per hour passing through a tunnel, or
 = 8.3 unscheduled requests per day for a particular social service. = 8.3 unscheduled requests per day for a particular social service.
| | 2. | The number of Poisson-type arrivals happening in any prespecified
time interval of fixed length is not dependent on the "starting time"
of the interval or on the total number of Poisson arrivals recorded
prior to the interval. For instance, if water-main breakdowns occur
as a Poisson process, the number of breakdowns occurring in a
particular day does not depend on the day being the tenth day of
the month versus, say, the twentieth day of the month; nor does it
depend on the number of breakdowns that occurred on the previous day
or in the previous week.
| | 3. | The numbers of arrivals happening in disjoint time intervals are
mutually independent random variables. Referring again to watermain
breakdowns, say that we were interested in the number of breakdowns
on September 28; this assumption would imply that knowledge (even
partial knowledge) of the numbers of breakdowns on any days or
combination of days other than September 28 would tell us nothing
about the number of breakdowns on the 28th.
| | 4. | Given that one Poisson arrival occurs at a
particular time, the
conditional probability that another occurs at exactly the same time
is zero. Thus, two or more arrivals cannot occur simultaneously. This
may or may not be a good model for water-main breakdowns, but it
certainly is not valid for the number of persons injured in auto
accidents; given that an auto accident occurs at a particular time,
it is an unfortunate fact that two or more persons may be injured at
once. |
These same four postulates can be stated mathematically more precisely:
| 1. | The probability that at least one Poisson arrival occurs in a time
period of duration
 is
is
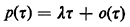
where o( ) is a generic expression for a term
or collection of terms that "goes to zero faster than k ) is a generic expression for a term
or collection of terms that "goes to zero faster than k as as  goes to zero" (for any constant k). Mathematically, goes to zero" (for any constant k). Mathematically,
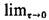 o( o( )/ )/ = 0. Note that for any finite sum of terms
oN( = 0. Note that for any finite sum of terms
oN( ) = o1( ) = o1( ) + o2( ) + o2( ) + . . . +
oN( ) + . . . +
oN( ) such that oj( ) such that oj( )/ )/ 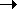 0 as 0 as  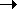 0 (j = 1, 2, . . ., N), we have 0 (j = 1, 2, . . ., N), we have 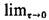 oN( oN( ) ) = 0. = 0.
|
2. | Let N(t) = total number of Poisson arrivals occurring in the interval [0, t].
We assume that N(0) = 0. For the interval {t1, t2}, the number of Poisson-type
arrivals [N(t2) - N(t1)] (t2 >
t1 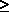 0) is dependent only on (t2 - t1) and not
on t1 or N(t1). 0) is dependent only on (t2 - t1) and not
on t1 or N(t1).
| |
3. | If 0  t1 < t2 t1 < t2  t3 < t4
t3 < t4  . . ., the numbers of arrivals occurring in
disjoint time intervals [N(t2) - N(t1)],
[N(t4) - N(t3)], . . . are mutually
independent random variables. . . ., the numbers of arrivals occurring in
disjoint time intervals [N(t2) - N(t1)],
[N(t4) - N(t3)], . . . are mutually
independent random variables.
| |
4. | The probability that two or more Poisson arrivals occur in a time
interval of length  is o( is o( ). ).
| |
Given postulates 1-4, we now wish to prove the fundamental result for a
Poisson process: that the number of Poisson arrivals occurring in a time
interval of length t is Poisson-distributed with mean
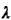 t: t:
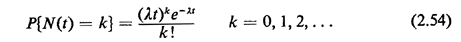
Armed with this result, we can derive all the other interesting properties
of a Poisson process.
Proof of (2.54): Let Pm(t) denote the probability that exactly m arrivals
occur in time t,
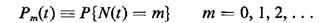
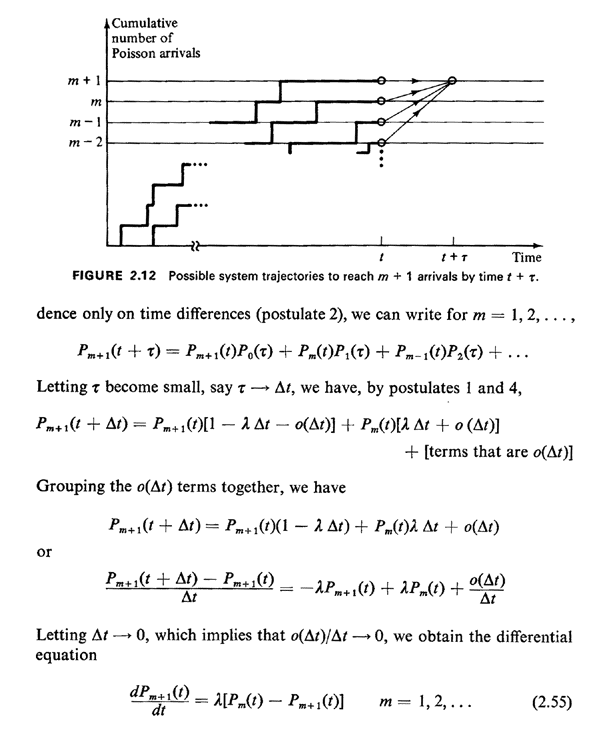
We consider the time interval [0, t] and expand it by an amount
 as shown in Figure 2.12. We are interested in the probability that exactly m + 1
Poisson arrivals have occurred by time t +
as shown in Figure 2.12. We are interested in the probability that exactly m + 1
Poisson arrivals have occurred by time t +  As shown in Figure 2.12, this
event could occur with m + 1 arrivals occurring in [0, t] and no arrivals
in [t, t +
As shown in Figure 2.12, this
event could occur with m + 1 arrivals occurring in [0, t] and no arrivals
in [t, t +  ], or m arrivals in [0, t] and 1
arrival in [t, t + ], or m arrivals in [0, t] and 1
arrival in [t, t +  ], and so on. Invoking independence of nonoverlapping intervals (postulate 3) and
depen ], and so on. Invoking independence of nonoverlapping intervals (postulate 3) and
depen
This equation makes sense intuitively: it states that the
time rate of change of the probability of exactly m + 1 arrivals
by time t is equal to the probability of exactly m arrivals in
time t multiplied by the rate at which a "transition occurs"
from m to m + 1 arrivals, minus the probability of already
having m + 1 arrivals by t multiplied by the rate at which
a transition occurs from m + 1 to m + 2 arrivals; the
conditional transition rate in each case is  . Similar logic can be used to develop sets of coupled
differential equations for more complicated processes, say where . Similar logic can be used to develop sets of coupled
differential equations for more complicated processes, say where  is dependent on the number of previous arrivals or perhaps where
arrivals can "depart," as in queueing systems. These ideas are
expanded further in the discussion of "birth" processes in Chapter 3
and "birth-and-death" processes in Chapter 4. is dependent on the number of previous arrivals or perhaps where
arrivals can "depart," as in queueing systems. These ideas are
expanded further in the discussion of "birth" processes in Chapter 3
and "birth-and-death" processes in Chapter 4.
While (2.55) holds for m = 1, 2, . . ., we also require an equation
for m = 0. In a manner similar to the derivation above, we obtain

The intuitive interpretation here is directly analogous to that of
(2.55). The solution to (2.56) is clearly
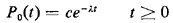
with the constant c determined by the initial condition that
P0(0) = 1, implying that c = 1. Then, by substitution into (2.55),
one proves by induction that

This completes the proof.
|



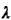 t:
t:
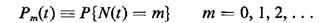
 as shown in Figure 2.12. We are interested in the probability that exactly m + 1
Poisson arrivals have occurred by time t +
as shown in Figure 2.12. We are interested in the probability that exactly m + 1
Poisson arrivals have occurred by time t +  As shown in Figure 2.12, this
event could occur with m + 1 arrivals occurring in [0, t] and no arrivals
in [t, t +
As shown in Figure 2.12, this
event could occur with m + 1 arrivals occurring in [0, t] and no arrivals
in [t, t +  ], or m arrivals in [0, t] and 1
arrival in [t, t +
], or m arrivals in [0, t] and 1
arrival in [t, t +  ], and so on. Invoking independence of nonoverlapping intervals (postulate 3) and
depen
], and so on. Invoking independence of nonoverlapping intervals (postulate 3) and
depen
 . Similar logic can be used to develop sets of coupled
differential equations for more complicated processes, say where
. Similar logic can be used to develop sets of coupled
differential equations for more complicated processes, say where  is dependent on the number of previous arrivals or perhaps where
arrivals can "depart," as in queueing systems. These ideas are
expanded further in the discussion of "birth" processes in Chapter 3
and "birth-and-death" processes in Chapter 4.
is dependent on the number of previous arrivals or perhaps where
arrivals can "depart," as in queueing systems. These ideas are
expanded further in the discussion of "birth" processes in Chapter 3
and "birth-and-death" processes in Chapter 4.