


2.12.3 Unordered Arrival TimesWe now know that arrivals occur singly in a Poisson process with interarrival times between successive arrivals distributed as negative exponential random variables. But suppose that we turn things around a bit and say that we have waited through the interval [0, t] and that exactly m Poisson arrivals have occurred in [0, t]. And, rather than queue up in some orderly fashion (like first arrivals first in line), all the arrivals are mixed together, such as the students sitting in a classroom or the patients sitting in the waiting room of an outpatient clinic. We wish to derive a property of the Poisson process which in part is responsible for its nickname "most random of random processes." We call the in arrivals the unordered arrivals of a Poisson process, since they are not ordered in accordance with the time of their arrival. We wish to determine the probabilistic behavior of the in unordered arrival times. To do this, we partition the interval [0, t] into 2m + 1 arbitrary subintervals ai and bi, as shown in Figure 2.13. Suppose that we are interested in the event Em that exactly one arrival occurred in each of the subintervals bi and that no arrival occurred in any of the subintervals ai. We wish to calculate the probability of Em occurring, given that exactly m arrivals occurred in [0, t]. 
(Clearly, the probability of Em is zero for any numbers of arrivals other than m.) Thus, invoking the definition of conditional probability, we want 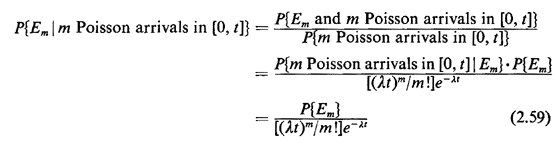
But Em is the union of 2m + 1 events that, by the Poisson postulates, are mutually independent. For m of the events, we want the probability of exactly one arrival in a subinterval bk, and this is simply 
But suppose that the process had been one in which we took each potential arrival, say a person, and "tossed" him/her "at random" into the interval [0, t], with successive tosses being independent. The probability that any particular arrival "ends up" in interval bk is then simply bk/t, since the arrival time of such a person is uniformly distributed over [0, t]. The probability  that the m arrivals distributed over [0, t] in this way each end
up as the single occupant of one subinterval bk is then simply that the m arrivals distributed over [0, t] in this way each end
up as the single occupant of one subinterval bk is then simply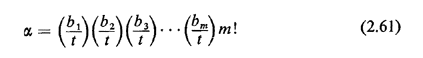
where the factorial term arises from the number of distinct ways in which the arrivals could be situated in the subintervals; that is, there are m! points in the experiment's sample space having the property we desire, and each point has the same probability. Since (2.60) and (2.61) are identical, we thus have derived the following result: the unordered arrival times in a Poisson process are independently, uniformly distributed over the fixed time interval of interest. |