


2.13 RANDOM INCIDENCEThe Poisson process is one of many stochastic processes that one encounters in urban service systems. The Poisson process is one example of a "point process" in which discrete events (arrivals) occur at particular points in time. For a general point process having its zeroth arrival at time T0 and the remaining arrivals at times T1, T2, T3, . . ., the interarrival times are 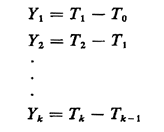
Such a stochastic process is fully characterized by the family of joint pdf's 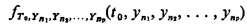 for all integer values of p and all possible combinations of
different n1, n2, . . ., where each ni is a positive integer
denoting a particular interarrival time. Maintaining the
depiction of a stochastic process at such a general level,
although fine in theory, yields an intractable model and one
for which the data (to estimate all the joint pdf 's) are
virtually impossible to obtain. So, in the study of stochastic
processes, one is motivated to make assumptions about this
family of pdf's that (1) are realistic for an important class
of problems and (2) yield a tractable model.
for all integer values of p and all possible combinations of
different n1, n2, . . ., where each ni is a positive integer
denoting a particular interarrival time. Maintaining the
depiction of a stochastic process at such a general level,
although fine in theory, yields an intractable model and one
for which the data (to estimate all the joint pdf 's) are
virtually impossible to obtain. So, in the study of stochastic
processes, one is motivated to make assumptions about this
family of pdf's that (1) are realistic for an important class
of problems and (2) yield a tractable model.We wish to consider here the class of point stochastic processes
for which the marginal pdf's for all of the interarrival times
(Yk) are identical. That is, we assume that 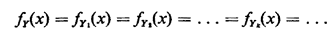
Thus, for Yk, if we selected any one of the family of joint pdf's fYn1,Yn2, . . ., Ynp (yn1, yn2, . . . , yk, . . ., ynP) and "integrated out" all variables except yk, we would obtain fY(.). Note that we have said nothing about independence of the Yk's They need not be mutually independent, pairwise independent, or conditionally independent in any way. For the special case in which the Yk's are mutually independent, the point process is called a renewal process. The Poisson process is a special case of a renewal process, being the only continuous-time renewal process having "no memory." However, the kind of process we are considering can exhibit both memory and dependence among the inter-event times. In fact, the dependence could be so strong that once we know the value of one of the Yk's we might know a great deal (perhaps even the exact values) of any number of the remaining Yk's.
In situations such as these, for which we know fY(.) or at least the mean and variance of Y, we are often interested in the following problem. An individual, say a potential bus passenger or a homeowner looking for a police patrol car, starts observing the process at a random time, and he or she wishes to obtain the probability law (or at least the mean) of the time he or she must wait until the next arrival occurs. In various applications this time could be the waiting time for a bus, subway, or elevator or the time until arrival of a patrol car. This is said to be a problem of random incidence, since the individual observer is incident to the process at a random time. The random time assumption is important: the time of random incidence of the observer can in no way depend on the past history of actual arrival times in the process. We now derive the probability law for V, the time from the moment of random incidence until the next arrival occurs. We do this for continuous random variables since the same reasoning applies in the discrete case. The derivation proceeds in stages, first conditioning on W, the length of the interarrival gap entered by random incidence. For instance, the gap in which a potential bus passenger arrives has length equal to the sum of two time intervals: (1) the time between the arrival of the most recent bus and the arrival of the potential passenger, and (2) the time between the passenger's arrival and the arrival of the next bus. We now argue that the probability that the gap entered by random incidence assumes a value between w and w + dw is proportional to both the relative frequency of occurrence of such gaps fY(w)dw and the duration of the gap w. That is, 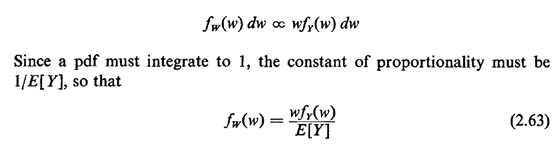
This result says that random incidence favors gaps of longer duration in direct proportion to their duration. The argument for this result is most simply given by example. Given two gap lengths w1 and w2 = 2w1 for which the relative frequencies are identical [fY(w1)dw = fY(w2)dw], then one is twice as likely to enter the gap of length 2w11 compared to the gap of length w1. Or, given the same two gap lengths, w1 and w2 = 2w1, for which the relative frequency of the large gap length is only half that of the smaller [fY(w2)dw = (1/2)fY(w1)dw], we are equally likely to enter either of the two types of gaps; here the doubling of relative frequency for w, "makes up for" the doubling of duration of w2. Now, given that we have entered a gap of length w by random incidence, we are equally likely to be anywhere within the gap. More precisely, there is a constant probability of being in any interval  to to  + h for any fixed h > 0,
assuming that [ + h for any fixed h > 0,
assuming that [ , ,  +
h] is fully contained within the gap. Thus, given w, the time until gap completion (i.e., the time until the
next event) has a uniform pdf: +
h] is fully contained within the gap. Thus, given w, the time until gap completion (i.e., the time until the
next event) has a uniform pdf: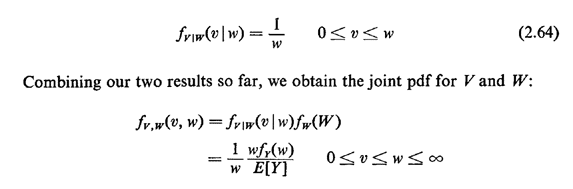
The marginal for V, which is what we want, is formed simply by "integrating out" W, 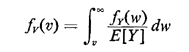
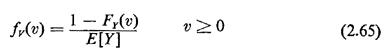
Question: Assuming that FY(O) = 0, does this result make intuitive sense for values of v near zero?
|