


2.2 EVENT PROBABILITIESThe second step in constructing a probabilistic model is to assign probabilities to events in the sample space. For any arbitrary event A, we say that P{A} is the probability that an outcome of the experiment is contained or included in event A. This is a clearer statement than saying that P{A} is the "probability of event A occurring," a statement that sometimes leads to confusion. Unless event A is a single point in the sample space, event A never "occurs" in its totality, but rather a single element or point in A may be the outcome of a particular experiment. The assigned event probabilities must obey the three axioms of probability: 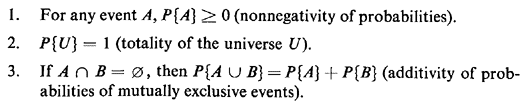
For the moment we will not be concerned with the method of assigning probabilities. We will assume that these probabilities are assigned to each finest-grained outcome of the experiment so that for each event A one can compute P{A} by simply summing the probabilities of the finest-grained outcomes comprising A. As we will see shortly, this summation could entail the sum of a finite number of elements or a countably infinite number of elements (in a countably infinite sample space), or it could entail integration (in a noncountably infinite sample space). Sometimes we have conditioning events in a sample space, reflecting partial information about the experimental outcome, and we wish to know what this means about the likelihood of other events "occurring or not occurring," given the conditioning event. Thus, we define conditional probability as 
Given that the conditioning event requires that the collection of "B-type" outcomes that could occur must also be contained in A, we could rewrite the definition of conditional probability as 
In manipulating conditional probabilities, the set of outcomes contained in the conditioning event A now constitutes the universal set of outcomes. Where "before the fact" (of A) the a priori universe was U, "after the fact" the a posteriori universe is A. Given the conditioning event, the new universe A is to be treated just as a sample space. Thus, the probabilities distributed over the finest-grained outcomes in A must be scaled so that their total (conditional) probability sums to 1. To do this, any event C that is fully contained inA (i.e.,A  C = C or A C = C or A
 C = A)
must have its corresponding probability scaled by 1/P{A}. Thus, C = A)
must have its corresponding probability scaled by 1/P{A}. Thus,

This is the operational definition of conditional probability. When dealing with the intersection of events, we will on occasion substitute a comma for the intersection operator. As an example, given two conditioning eventsA1 and A2, P{B|A1  A2} and P{B|A1, A2}
have the same meaning: the probability that the experimental
outcome is contained in event B, given that it is contained in both
A1 and A2 A2} and P{B|A1, A2}
have the same meaning: the probability that the experimental
outcome is contained in event B, given that it is contained in both
A1 and A2Two events are said to be independent if information concerning the occurrence of one of them does not alter the probability of occurrence of the other. Formally, events A and B, with P{A} > 0 and P{B} > 0, are said to be independent if and only if 
In other words, for each possible event A, information on the occurrence of any combination of the other events does not affect the probability that the experimental outcome is contained in event A, It is important to be aware that events may be pairwise independent or be otherwise conditionally independent but not mutually independent. Only with mutual independence does "information about the 'other' events Aj, j  i,
tell us nothing about event Ai" i,
tell us nothing about event Ai" |