


2.5 CONDITIONAL PMF'S AND INDEPENDENCESuppose we are told that an experimental outcome is contained in event A. We then wish to explore the probabilistic behavior of random variables X and Y, given A. Following the definition of conditional probability, we introduce the conditional compound pmf, 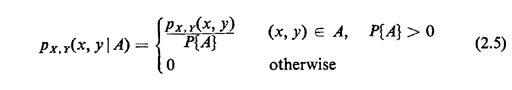
If event A is stated in terms of the specific experimental value of one of the random variables of the experiment, we introduce another notation: 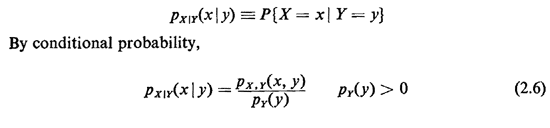
These notations and definitions extend in an obvious way to situations with more than two random variables. Example 2: Minibus Suppose that a minibus with capacity for five passengers departs from a commuter station. Observation has shown that the bus never departs empty (with no passengers) but that each possible positive number of passengers is equally likely to be on the bus at departure time. Passengers are of two types: male and female. Given that the departing bus contains exactly n passenger (n = 1, 2,..., 5), each possible combination of male and female passenger has been found to be equally likely. a. Identify the sample space and joint probability mass function for this experiment. b. Determine the marginal pmf for the number of females on the mini bus. c. Determine the joint conditional pmf for the number of females and the number of males on the minibus, given that the bus departs at full capacity. d. Determine the conditional marginal pmf for the number of females, given that there are at least twice as many females as males on the minibus. Solution: There are two random variables in this experiment: 
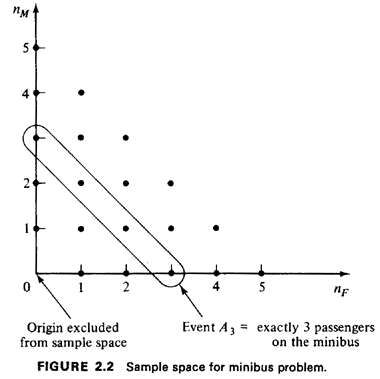
a. A complete listing of their possible (paired) values constitutes the sample space for this experiment. These points occupy the nearly triangular region shown in Figure 2.2. The region is not perfectly triangular since the origin (NF = 0, Nm = 0) is excluded because the minibus never departs empty. The region is bounded above by the line nf + nm = 5, which expresses the capacity constraint for the minibus. To determine the joint pmf for Nf and Nm, we must use the conditional information given in the word statement. We know that any particular positive total number of passengers, ranging up to 5, is equally likely. Let Ai = event that i total passengers are on the bus We know that P{A1} = 1/5, i = 1, 2,. .., 5. Points in an event Ai lie on the line nF + nm = i, as shown for A3 in Figure 2.2. Given that an outcome of the experiment is contained in event Ai, we know that each of the points in Ai is equally likely. Since the number of points in Ai is equal to i + 1, we have 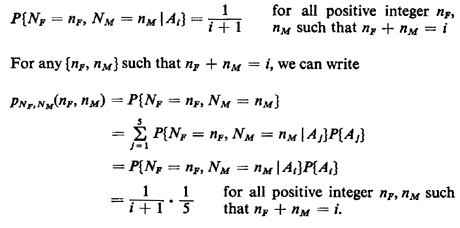
This is the answer to part (a). It says, roughly, that the probability that {Nf = nf and Nm = nM} is equal to 1/5 divided by 1 plus the sum nF + nm. For i = 3, for instance, 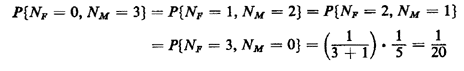
The complete joint pmf is shown in Figure 2.3. b. Once we have the joint pmf for NF and Nm, we can readily answer any question about the experiment. The marginal pmf for NF is found by invoking (2.4), which simply asks us to sum over all values of NM at each particular fixed value for NF. For instance, to obtain P{Nf = 3) = PNf(3), we sum the probabilities corresponding to the (finest-grained) events {Nf = 3, Nm = 0), {Nf = 3, Nm = 1}, and {Nf = 3, Nm = 2}, yielding 1/20 + 1/25 + 1/30 = 37/300. The complete pmf is shown in Figure 2.4. c. If we are given conditional information that the bus departs at full capacity, we know that the experimental outcome is contained in event As (i.e., nF + nm = 5). Thus, invoking (2.5), 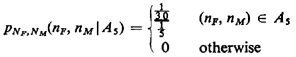
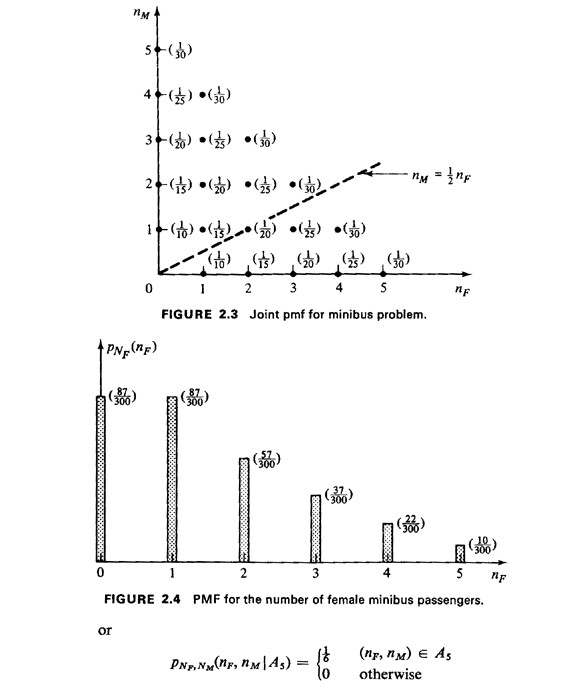
This corresponds to a straight line of probability masses, each having mass 1/6, at the integer points on the line nF + nm = 5 (nF, nm 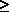 0). 0).d. Let B = event that "there are at least twice as many females as males on the minibus" We want PNf(nf | B). First we work in the original joint sample space to determine finest-grained outcomes contained in the event B. Clearly, these are points nF, nm satisfying the inequality 2nm  nF.
This corresponds to points lying on or below the line nm = I nF (shown
in Figure 2.3). Summing the probabilities of the eight finestgrained
outcomes satisfying this inequality, we find that P{B} = 124/300 = 31/75.
Then, to find the conditional marginal pmf for NF, given B, we
Simply sum the probabilities at a fixed value for nF over all values
of nm contained in B, then scale by 1/31/75. For instance, nF.
This corresponds to points lying on or below the line nm = I nF (shown
in Figure 2.3). Summing the probabilities of the eight finestgrained
outcomes satisfying this inequality, we find that P{B} = 124/300 = 31/75.
Then, to find the conditional marginal pmf for NF, given B, we
Simply sum the probabilities at a fixed value for nF over all values
of nm contained in B, then scale by 1/31/75. For instance,
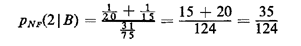
The entire conditional marginal pmf is displayed in Figure 2.5. Notice how the conditional information has shifted the pmf for NF toward greater numbers of females (compare to Figure 2.4). 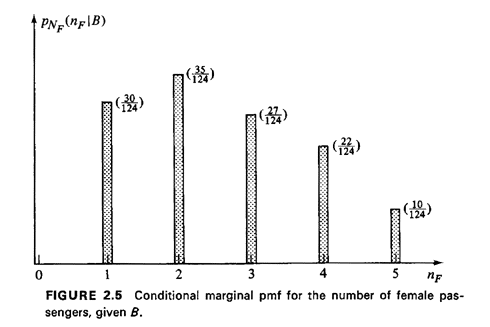
Just as events can be independent, so, too, can random variables be independent. Intuitively, if X and Y are independent, any information regarding the value of one tells us nothing new about the value of the other. Formally, random variables X and Y are independent if and only if PY|X(y | x) = py(y) for all possible values of x and y. Exercise 2.4: Independence of Random Variables Show that the definition of independence of X and Y implies that px|y(x|y) = px(x)and px,y(x,y) = px(x)py(y) for all possible values of x and y (2.7)Given an arbitrary number N of random variables, they are said to be mutually independent if their joint pmf factors into the product of the corresponding N marginal pmf's. Sometimes random variables may be independent but conditionally dependent; or, they may be dependent but conditionally independent. The definition of conditional independence is just what we expect: random variables X and Y are said to be conditionally independent given event A if and only if 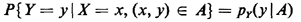
Exercise 2.5: Conditional Independence Show that for two random variables X and Y that are conditionally independent given event A, 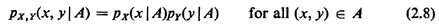
Example 2: (continued) In the minibus example, argue that Nf and Nm are not independent. Does there exist any nontrivial event A such that, given A, Nf and Nm are conditionally independent? |