


2.7 EXPECTATIONSuppose that we have an experiment with random variable X and a function of X, Y = g(X), which is itself a random variable. By this we mean that every experimental value x of the random variable X yields an experimental value g(x) for the random variable g(X) = Y. Then the expectation or expected value of g(X) is defined to be 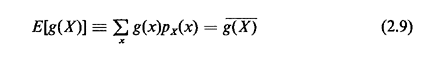
The conditional expected value of g(X), given the experimental outcome is contained in event A, is 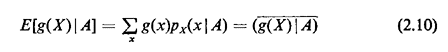
A key motivation for these definitions arises from large-sample theory, which reveals that if the experiment is performed independently many times, the empirically calculated average value of g(·) will probably be "very close to" E[g(X)].3 There are other motivations, too, such as z- and s-transforms, as we will see shortly. Unfortunately, the word expectation or expected value of a random variable is perhaps one of the poorest word choices one encounters in probabilistic modeling. In practice, these words are often used interchangeably with average or mean value of a random variable. The problem here is that the mean or expected value of a random variable, when considered as a possible experimental value of the random variable, is usually quite unexpected and sometimes even impossible. For instance, a flip of a fair coin with "tails" yielding X = 0 and "heads" X = I results in an expected value E[X] = 1/2, an impossible experimental outcome. Still, use of the term "expected value" persists and has caused considerable confusion in the minds of public administrators when reading consultants' reports or being briefed by unwary technical aides. Two particular functions g(X) will be of special interest in our work: 1. g(X) = X yields the mean value or expected value of the random variable X, 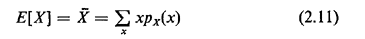
2. g(X) = (X - E[X])2 yields the variance or second central moment of the random variable X, 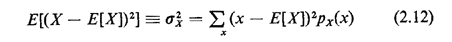
Here 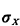 , which is the square root of the variance, is the standard
deviation of the random variable X. , which is the square root of the variance, is the standard
deviation of the random variable X.Exercise 2.6: Expected Value of a Sum Show that the expected value of the Sum of two arbitrary random variables X and Y is the sum of the two individual expected values (i.e., E[X + Y] = E[X] + E[Y]). Exercise 2.7: Variance in Terms of Moments Show that 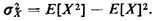
Exercise 2.8: Variance of a Sum Show that for two independent random variables X and Y, the variance of the sum is the sum of the two individual variances(i.e. 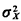 +y = +y =
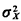 + + 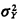 ). ).Exercise 2.9: Expected Value of a Product Suppose that X1, X2, ..., Xn. are mutually independent random variables. Let 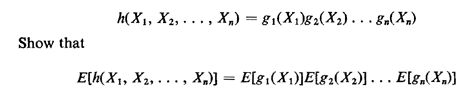
3 For this statement to be true, g(X) has to be "well behaved," where goodness of behavior usually implies that E[g2(X)] be finite. |