2.9.1 Bernoulli PMFA random variable X whose probability law is a Bernoulli pmf can take on only two values, 0 and 1: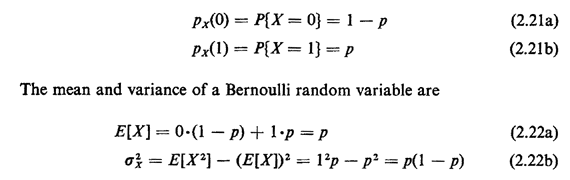 
The z-transform is ptx(z) = (I - p) + pz. The Bernoulli pmf arises in simple trials having only two outcomes; it is also useful in the analysis of setindicator random variables (see Section 3.3). As an example of the use of a Bernoulli pmf, consider a police car performing "random" patrol. Each hour (on the hour) the patrol officer spins a wheel of fortune on the car's dashboard to see if the car should patrol a specially designated "high-crime zone" during the next hour. If police crime analysts have determined that approximately 25 percent of the time on random patrol should be spent in this zone, then an angle equal to  /2 on the wheel
of fortune will be designated, "Patrol next hour in high-crime zone."
Here the "patrol indicator" random variable X equals I if the car
patrols the next hour in the high-crime zone; otherwise, X = 0. The
expected value for X is E[X] = p = 0.25. The variance is p(1 - p) =
(0.25)(0.75) = 0.1875. Each hour a separate (independent) experiment
is performed. Thus, the total number of hours that the high-crime
zone is patrolled during an 8-hour period is the sum of the
individual X's corresponding to each hour. The idea of such a
sequence of Bernoulli experiments will be developed further with
the next two pmf's. |