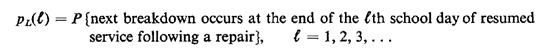Problems
The exercises contained within this chapter have been designed to give
the reader needed review experience in formal manipulation in
probabilistic analysis. The following four problems have the dual
purpose of continuing such review and providing experience in the
modeling of physical situations that typically arise in urban analysis.
The reader is also referred to Problem 3.1 for more review on the basic
concepts of probability modeling.
2.1 Discrete random variables: a clean sweep A 300-foot-long city block
face contains eight 25-foot-long parking spaces, as shown in Figure P2.
1. For convenience, we have numbered the parking spaces consecutively
from 1 to 8. Each Tuesday at 8:00 A.M. a street sweeper attempts to
clean the entire street. Any cars parked in those spaces inhibit the
work of the sweeper and are, accordingly, each given a $25 fine (parking
ticket). We assume that the probability that any given parking space
will be occupied by an illegally parked car is p and that the status
(full or empty) of each parking space is independent of the status of
all other parking spaces.
| a. | For any given Tuesday morning, determine
the mean and variance of
the number of illegally parked cars on this block face.
| | b. | Repeat part (a) for the mean and variance of the total dollar
value of parking tickets issued.
|
For each parked car, the sweeper is unable to sweep the 25 feet
contained within that car's parking space and, in addition, because of
maneuverability problems, it is unable to sweep within 12.5 feet on
either side of that car's parking space (we ignore
size differences of cars here). For instance, if cars were only parked
in spaces 1 and 3, the sweeper would be unable to sweep 100 consecutive
feet of the street, starting at x = 37.5 feet (see Figure P2.1).
| c. | Determine the probability of a clean
sweep of the street (i.e.,
that no illegally parked cars are present).
| | d. | Given that there are exactly two illegally parked cars on the
street, determine the conditional pmf for the length (in feet) of street swept.
| | e. | Find the unconditional mean length of street swept.
|
Hint: Avoid "brute-force" methods by arguing as follows: for any
"interior" point x, 62.5 < x < 237.5, the probability that x will be
swept is (1 - p)2 Why? Then, the expected length of parking space 4 that
will be swept is 25(1 - p)2. Continuing this reasoning and including the
other "noninterior" points, you should find that the answer is 75 + 50(l
- p) + 175(1 - p)2 feet. (This line of reasoning utilizes ideas of
coverage that are explained more fully in Chapter 3.)
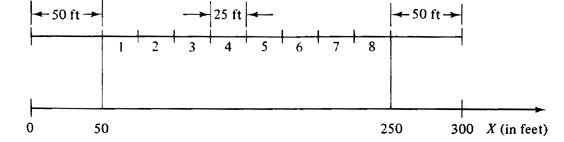
2.2 Mixed random variables: a shuttle Suppose that two buses, B1 and B2,
are used to shuttle passengers between two stations, S1 and S2, as shown
in Figure P2.2. For convenience, we denote the location x1
and x2 of
each bus B1 and B2, respectively, by its counterclockwise distance from
Sl, 0  x < 2 x < 2  .
We are given the following facts about system operation: .
We are given the following facts about system operation:
| 1. | Statistically, buses B1 and B2 behave
identically, as do stations S1 and S2.
| | 2. | Each bus spends 25 percent of its time at
station Sl, 25 percent at S2, and 50 percent traveling between the two stations.
| | 3. | Speed of travel is a fixed constant.
| | a. | Draw the cdf and pdf for the location of B1 at a randomly chosen
time. [If the cdf is differentiated to yield the pdf, any impulses that
result (associated with probability masses) are usually sketched as
spikes with numbers adjacent to the spikes equal to the corresponding
probability masses.]
|
For parts (b) and (c), assume that B1 and B2 operate completely
independently. (Is that reasonable?)
| b. | Sketch and describe the joint pdf for the locations of B1 and B2.
(You may have to extend to two dimensions your notion of impulses.)
| | c. | Define the headway H between B1 and B2 as the clockwise distance
from B1 to B2.

|
2.3 Poisson processes: subways are for waiting. Two one-way subway
lines, the A train line and the B train line, intersect at a transfer
station, as shown in Figure P2.3. A trains and B trains arrive at the
station according to independently operating
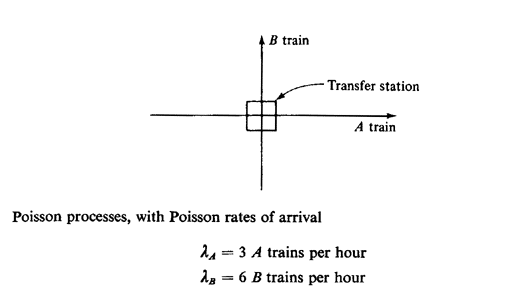
We assume that passenger boarding and unboarding occurs almost
instantaneously, not unlike true rush-hour conditions in many cities
throughout the world!
| a. | At a random time, Bart, a prospective passenger,
arrives at the
station, awaiting an A train.
| | i. | What is the pdf for the time he will have to
wait?
| | ii. | What is the probability that at least
3 B trains will arrive
while Bart is waiting?
| | iii. | What is the probability that exactly 3 B
trains will arrive
while Bart is waiting?
| | b. | What is the probability that the station
handles exactly 9 trains
during any given hour?
| | c. | If an observer counts the number of trains
that the station
handles each hour, starting at 8:00 A.M. on Tuesday, what is the
expected number of hours until he or she will first count exactly 9
trains during an hour that commences "on the hour"? (e.g., 9: 00 A.M.,
10: 00 A.M., 2: 00 P.M.)
| | d. | Whenever an A train is ready to depart from the station, it will
be held if an approaching B train is within 30 seconds of the station.
This delay policy is to facilitate the rapid transfer of passengers from
the B train to the A train.
| | i. | Approximately what fraction of A trains are
delayed in this
manner?
| | ii. | Given a B-train passenger who benefits from such instantaneous
transfer to an A train, using the up-to-30-second-delay policy for the A
train, compute his or her mean waiting time reduction and compare to the
mean increase in travel time for an already boarded A train passenger.
Intuitively, under what conditions would such a delay policy provide net
global travel-time reduction?
|
2.4 Discrete random incidence: school-bus repair Suppose that school
buses undergo maintenance only when they break down. For simplicity, we
assume that breakdowns occur only at the end of the school day after the
driver has driven all the students back to their home neighborhoods.
When repairs and other maintenance are completed (requiring at least one
day), each school bus behaves as a "new" bus with
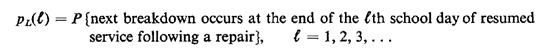
Whenever the bus servicing a route has broken down at the end of the
previous day, it is replaced by a recently repaired bus that has
probability pL(1) of breaking down at the end of its first day back in
service, pL(2) of breaking down at the end of its second day, and so on.
Each bus has a unique identification number painted boldly on its sides.
| (a) | Suppose that on some random day a parent starts accompanying his
or her child each day to the school bus stop. Show, by using arguments
of random incidence, that the pmf for the number of school days N until
the parent sees a different bus on the route (due to a breakdown of the
first bus) is
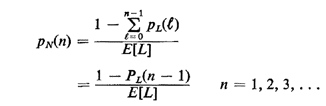
Hint: Follow directly the line of reasoning used in developing
(2.63)-(2.65). Note that at least one day is required to observe a new
bus.
This is a case of discrete random incidence, since the random variables
involved - the time between events (breakdowns) and the time from random
incidence until the next event (N) - can assume only nonnegative integer
values.
| | (b) | Explain intuitively the result pN(1) = 1/E[L].
| | (c) | Following the conditioning argument used to derive (2.66), show
that
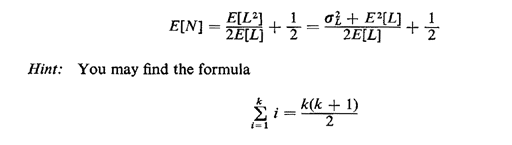
useful. Does the addition of the "1/2" term make sense intuitively?
Evaluate E[N] assuming that E[L] = 50 days and 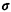 L = 30 days. L = 30 days.
|
|




 x < 2
x < 2  .
We are given the following facts about system operation:
.
We are given the following facts about system operation: