


3.2.3 Perturbations to a Sample SpaceAs a last example of the use of perturbation ideas, consider a sample space S associated with the location (X, Y) of an object. We will assume that the object is uniformly distributed over S. Suppose that we perturb the sample space by the addition and subtraction of a term,
For our development here, 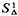 and
and 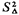 must have equal area.
However, the ideas can be extended to more general
situations. must have equal area.
However, the ideas can be extended to more general
situations.Now if we are interested in means and variances of some function of (X, Y), say g(X, Y), we can apply reasoning analogous to that used in the previous two sections. We assume now that the object is distributed uniformly over S'. Exercise3.3 Defining P  appropriately, show that appropriately, show that
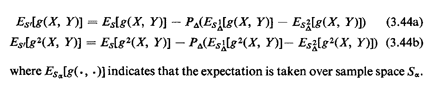
Example 8: Single Facility Location Consider the peculiarly shaped region in Figure 3.16. Assume that a facility is to be placed somewhere within the region, say at point (x0, y0). Demands for service are distributed independently and uniformly throughout the region. Then, either a server ("response unit") travels from (x0, y0) to the location of the service demand, at point (X, Y), or the person at (X, Y) travels to the facility at (x0, y0). In either case, the travel distance for a service request is 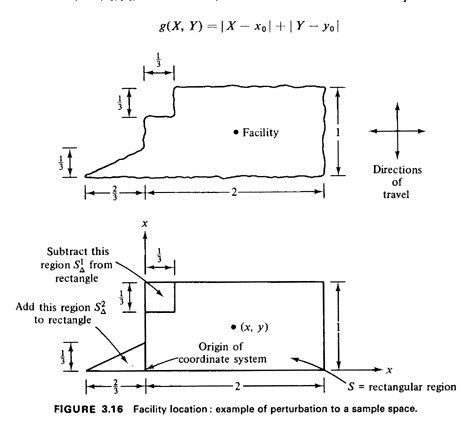
We wish to locate the facility in order to minimize the expected travel distance Efg(X, Y)]. Solution The peculiar region can be thought of approximately as a rectangular region S plus the triangular region 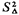 minus the
square region minus the
square region 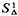 (see Figure 3.16). By methods discussed
previously, (see Figure 3.16). By methods discussed
previously,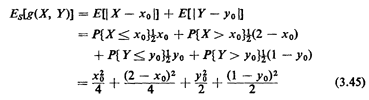
By calculating areas and recognizing that the area of the rectangle is 2, 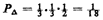
To calculate the two perturbation terms, let us assume (for the moment) that x0 > 1/3 and 1/3  y0 y0
 2/3; we can check our final
result with these inequalities. Then, by integration or by
inspection,5
2/3; we can check our final
result with these inequalities. Then, by integration or by
inspection,5
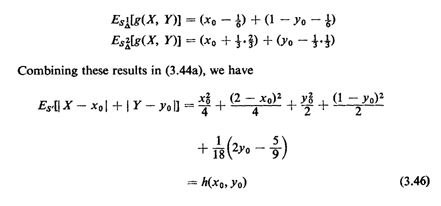
Taking the derivative with respect to xO and setting it equal to zero, we find that the optimal x-location is 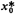 = 1, which is
identical to that of the rectangle alone. Does this make
intuitive sense? Taking the derivative with respect to yO and
setting
it equal to zero, the optimal y-location is
= 1, which is
identical to that of the rectangle alone. Does this make
intuitive sense? Taking the derivative with respect to yO and
setting
it equal to zero, the optimal y-location is 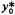 = 4/9, a shift
downward of about 11 percent compared to
= 4/9, a shift
downward of about 11 percent compared to 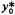 =1/2
for the rectangle. Does this make intuitive sense? =1/2
for the rectangle. Does this make intuitive sense?
Summarizing, the location for the facility that minimizes mean
travel distance to and/or from it is ( |