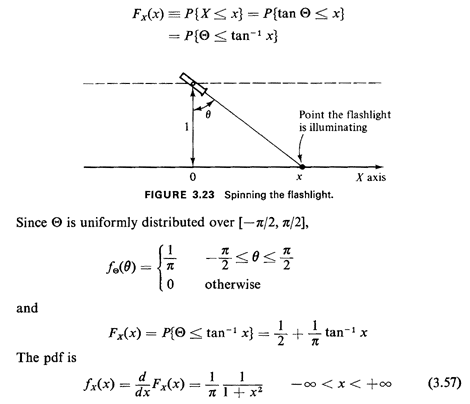
3.3.3 Cauchy Distribution

As illustrated above, many geometrically oriented problems require deriving the distribution of a function of one or more random variables. Often the original random variable(s) is (are) uniformly, independently distributed over some range of values, perhaps depicting position or angle of an object. One simple example gives rise to an unusual probability law, the Cauchy distribution.

Suppose that Buffon's needle were, in fact, a narrow-beam flashlight rather than a needle. The flashlight is spun around its center, located unit distance from the x-axis (Figure 3.23). After the flashlight has stopped spinning, we are interested in the point X on the x-axis at which the flashlight is pointing. If it is not pointing toward the x-axis, we repeat the spinning trial as many times as necessary until it does. This situation might, in fact, correspond to a method for choosing (1) a point for random inspection along a pipeline, (2) a volunteer standing in a line of personnel at "rollcall," or (3) a "winner" in a "straight" version of spin- the-bottle.

As shown in Figure 3.23 the point X is determined by the angle of the flashlight, -/2 /2, since X = tan . From the physical situation we may assume that is uniformly distributed over [-/2, /2]. We proceed with the never-fail method to derive the probability law of X,



This is the Cauchy probability density function. It possesses the interesting property that its variance is infinite (since th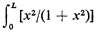e integral tends to L as L becomes large). In fact, to be mathematically precise, the mean of the Cauchy density function is also undefined since the integral 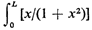dx tends to n L as L becomes large. Thus, a perfectly valid random variable need not possess well-defined or finite means and variances.

Problem 3.17 asks you to explore certain additional properties of the Cauchy distribution.