3.7.1 Simple Model
Example 12: Design of a Response Distfict
Suppose that we have once more the situation described in
Exercise 3.1, where requests
for assistance are medical emergencies and the urban response unit
is an ambulette. Under
the assumptions that (1) locations of a medical emergency
(X1,
Y1) and of the ambulette
(X2,
Y2) are independent and
uniformly distributed
over the response district, and (2) travel is parallel to the sides
of the rectangular
response area, the travel distance [from (3.11)] is given by
D =
|X1 -
X2|
+ |Y1 -
Y2|
From Exercise 3.1, we then have that
E[D) = 1/3[Xo + YJ
(3.12a)
where X0 and
Y0
are the sides of the rectangle (see Figure 3.3). In this example we
wish to formulate and
solve the problem of optimal district design and to investigate the
sensitivity of our
results to suboptimal designs.
Solution
To find the district dimensions which lead to the
minimum expected travel
distance, we must keep the area of the response district
A0 =
X0
Y0 constant and minimize
(3.12a) subject to the
condition YO =
AO/XO.
Without this constant, a zero area (point) district would be
optimal, an obviously
infeasible result considering that the collection of districts in a
city must usually
cover the entire city (which has fixed positive area). Not
surprisingly, (3.12a) is
minimized when the rectangle becomes a square,

More generally, if the effective travel speeds in
the x-direction and
the y-direction, vx and
vy,
are independent of travel distance, the expected travel time,
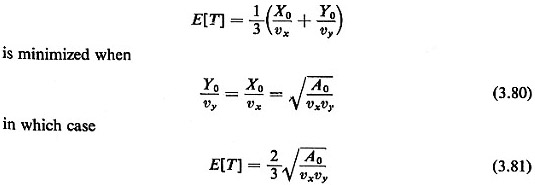
Intuitively speaking, the optimal shape of the
district, as given by
(3.80), is the one for which it takes as much time to traverse the
district from
"east to west" as from "north to south."
The expressions for E[D] and E[T] turn out to
be "robust"
(i.e., rather insensitive to the exact values of
X0
and Y0). To see this, let
us examine the case
where
X0 =
 Y0
(3.82) Y0
(3.82)
where  is a positive constant.
Without loss of generality we
assume is a positive constant.
Without loss of generality we
assume  > 1 and, as before, we set
A0 =
X0
Y0. Then (3.12) can be
written as
> 1 and, as before, we set
A0 =
X0
Y0. Then (3.12) can be
written as

The second term in (3.83) is the amount by which E[D] deviates
from its minimum value in
(3.79). For 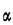 = 1.5 that term becomes equal
to 0.014, = 1.5 that term becomes equal
to 0.014,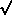 A0
(i.e., E[D] is only about 2 percent greater than its minimum
value). Even for A0
(i.e., E[D] is only about 2 percent greater than its minimum
value). Even for 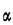 = 4, E[D]
is only 25 percent more than its minimum value. An entirely
similar analysis can
demonstrate the robustness of (3.80). = 4, E[D]
is only 25 percent more than its minimum value. An entirely
similar analysis can
demonstrate the robustness of (3.80).
Results such as those of (3.79) and (3.80) can
be derived for
various district shapes. The first three columns of Table 3-1
summarize the equivalents of
(3.79) for a square district, a square district rotated by 45' with
respect to the
right-angle directions of travel, and a circular district. The
following four cases are
included:8
- Euclidean (straight-line) travel when the response unit is
randomly and uniformly
positioned in the district.
- Case I with right-angle travel.
- Euclidean travel with the response unit located at the center
of the district.
- Case 3 with right-angle travel.
In all cases it is assumed that the locations of
requests for service
are uniformly distributed in the district and independent of the
location of the service
unit. When the constants in Table 3-1 are multiplied by
 , the
square root of the area
of the district in question, E[D] is obtained. In some instances
(e.g., a square district
with a randomly positioned response unit and Euclidean travel) the
constant of interest is
not known exactly and the best known approximation, to
two-decimal-place accuracy, is
shown. Some of these constants have already been derived in this
chapter or will be
derived in the Problems. , the
square root of the area
of the district in question, E[D] is obtained. In some instances
(e.g., a square district
with a randomly positioned response unit and Euclidean travel) the
constant of interest is
not known exactly and the best known approximation, to
two-decimal-place accuracy, is
shown. Some of these constants have already been derived in this
chapter or will be
derived in the Problems.

The three district geometries included in Table 3-1 are
"special
cases" of rectangular, diamond-shaped, and elliptic districts.
If one varies the
district dimensions of each type while constraining district area to
equal a constant A0,
E[D] is minimized by the symmetric geometries represented in Table
3-1.
It can be seen from Table 3-1 that, for any given
district area A, E[D]
is very insensitive to the exact geometry of the district. This can
be confirmed by
deriving E[D] for other possible district geometries, such as
equilateral triangles or
piece-of-pie-like sectors of circles. Moreover, for any given
district geometry, the value
of E[D] is insensitive to changes of the dimensions of the district
that might make it
appear to deviate appreciably from its optimum shape. This, too, can
be confirmed by
performing a sensitivity analysis similar to the one for the
rectangular district in
Example 12.
From these observations it can be concluded that
we can use the first
three columns of Table 3-1 to infer similar approximate expressions
for E[D] that apply to
districts of any shape as long as (1) one of the dimensions (e.g.,
"length") is
not much greater than the other dimension (e.g., width), and (2)
major barriers or
boundary indentations do not exist in the district. Districts that
satisfy both of the
conditions above will be called here, informally, "fairly
compact and fairly convex
districts." We can now state the following:
For fairly compact and fairly convex districts and
for independently and
spatially uniformly distributed requests for service,

where A0,, is the area of
the district and c is a
constant that depends only on the metric in use and on
the assumption regarding
the location of the response unit in the district.
The last column of Table 3-1 lists values that
can be used for c in
(3.84) for the four combinations of response unit locations and
metrics that we have
examined here. In all cases, we have selected the largest value of c
listed in each row of
the three leftmost columns of Table 3-1.
When the effective travel speed is independent of
the distance covered,
one can use the constants in the fourth column of Table 3-1 to
approximate the expected
travel time, E[T), as well. In that case we have

in the case of Euclidean travel (assuming that the effective travel
speed v is independent
of the direction of travel) and

for right-angle travel. In this latter case, the district
"compactness"
statement requires that
E[Teast-west] 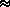 E[Tnorth-south]
E[Tnorth-south]
That is, it takes on the average about as much time
to traverse the
district from east to west as from north to south.
Another observation that can be made on the basis
of the foregoing
discussion is that both E[D] and E[T] are proportional to the square
root of the district
area, A0,, irrespective of
the specific distance
metric in use. This is hardly surprising since this relationship is
basically a
dimensional one: distance is the square root of area. More formally,
if the coordinates of
each point (x, y) in the district of interest are multiplied by 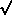 m (m > 1) [i.e.,
point (x, y) now
becomes point ( m (m > 1) [i.e.,
point (x, y) now
becomes point (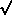 m
x, m
x, 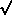 m y)], then
the area of the district increases m-fold but the length,
L, of any given
route between the pair of points
(x1,
y1,) and
(x2,,
y2,) in the
original
district-becomes equal to m y)], then
the area of the district increases m-fold but the length,
L, of any given
route between the pair of points
(x1,
y1,) and
(x2,,
y2,) in the
original
district-becomes equal to 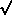 mL in the expanded district. mL in the expanded district.
Equivalently, we can state that E[D] and E[Tj
must be proportional to
the inverse of the square root of the density of response units in a
district, for
districts with more than one response unit. That is, if a district
of area A is divided
into n approximately equal fairly convex and fairly compact
subdistricts of responsibility
(whose shapes may vary), then

where y denotes the spatial density of service units. We shall
derive the same functional
type of relationship in a somewhat different context later in this
chapter [cf. (3.101a)
and (3.104a)].
8 few results for metrics other than Euclidean
or right-angle are
derived in the Problems. |