3.10 Ratio of right-angle and Euclidean travel
distances In this problem
we test the reasonableness of the isotropy assumption used in
Example 4. It is appropriate
to question this assumption since most service regions in a city are
such that 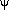 will not be uniformly
distributed between 0
and will not be uniformly
distributed between 0
and  /2. We consider
three cases. /2. We consider
three cases.

b. Case 2. Suppose that the square-unit-area service
area of part (a) is
rotated at a 45° angle to the directions of travel. In such a case
intuition might lead
one to think that E[R] would be less than 4/ . Why? To
investigate this conjecture it is
helpful to use the relationship . Why? To
investigate this conjecture it is
helpful to use the relationship
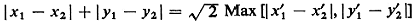
where the primed variables are defined relative to a coordinate
system rotated at 45°
with respect to the original coordinate system. Show that in such
a case
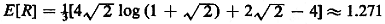
(Intuition is correct but the result is closer to 4/ than might
otherwise have been
expected.) than might
otherwise have been
expected.)
C. Case 3. Suppose that the mobile unit is located
uniformly on the perimeter
of a square rotated at 45° to the directions of travel. Suppose
that the unit travels in a
shortest (right-angle) distance manner to the center of the
square. Again, T is the angle
at which the directions of travel are rotated with respect to the
straight line connecting
the unit's initial position to the center of the square. Show that
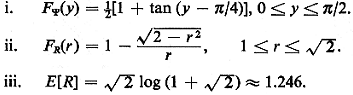
Do all the results for E[R] check with your intuition?
|