3.26 Space-time
Poisson process
Consider a highway that starts at x = 0 and extends
infinitely eastward toward
increasing values of x. Automobile accidents and breakdowns
occur along the
highway in a Poisson manner in time and space at a rate y per hour
per mile. Any accident
or breakdown that occurs remains at the location of occurrence until
serviced.
At time t = 0, when there are no
unserviced accidents or
breakdowns on the highway, a helicopter starts
from x = 0 flying
eastward above the highway at a constant speed s. As a
service unit, the
helicopter will land at the site of any accident or breakdown that
it flies over.
Moreover, given at time t the helicopter is located at x =
st, the helicopter can
be dispatched (by radio) to service any accident or breakdown that
occurs behind it (i.e.,
at values of x  st). We assume that any such
dispatch occurs
immediately after the accident or breakdown occurs. st). We assume that any such
dispatch occurs
immediately after the accident or breakdown occurs.
We are interested in the time the helicopter
first becomes busy, either
by landing at an accident/breakdown site or by being dispatched to
an accident/breakdown
behind its current position; in the latter case, the instant of
dispatch (not the time of
arrival at the scene) is the time of interest.
Let
T = time that the helicopter first becomes busy
a.
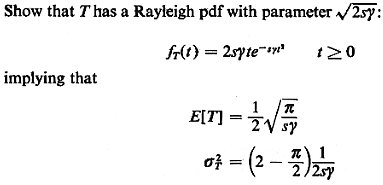
b. Let
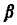  probability that the first
accident/breakdown is a dispatch
incident behind the helicopter probability that the first
accident/breakdown is a dispatch
incident behind the helicopter
1 - 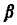  probability that the first
accident/breakdown occurs as a
result of patrol (i.e., the helicopter
discovers it) probability that the first
accident/breakdown occurs as a
result of patrol (i.e., the helicopter
discovers it)
Show that 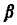 = 1 - = 1 - 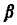 = 1/2. = 1/2.
Hint: Condition on the event that the first
accident breakdown occurs in
the time interval (t, t + dt).
c. Let
X  location of the first
accident/breakdown that the
helicopter services location of the first
accident/breakdown that the
helicopter services
Show that
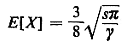
d. Suppose that
L1, =
time of first
accident/breakdown that the helicopter flies over, assuming that
it is no longer
dispatched by radio (i.e., all incidents are
helicopter-discovered incidents)
L2 = time of first
accident/breakdown that the
helicopter is dispatched to, assuming that it never services
accident/breakdowns that it
flies over
Then, for instance, T =
Min[L1,
L2].
Show that L1 and
L2
are identically distributed Rayleigh random variables, each with
parameter 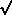 sy.
Finally, argue that L1
and L2
are independent, thereby concluding that the minimum of two
independent Rayleigh random
variables, each with parameter sy.
Finally, argue that L1
and L2
are independent, thereby concluding that the minimum of two
independent Rayleigh random
variables, each with parameter 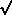 y, is itself a Rayleigh random
variable with
parameter y, is itself a Rayleigh random
variable with
parameter 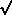 2y. 2y.
|