4.10.1 Important Property of M/M/m Queueing Systems
For M/M/m queueing systems with infinite queue
capacity, we now state a property that often plays an important simplifying role in the
analysis of queueing networks. It is sometimes referred to as the equivalence property for
M/M/m systems.
Let the arrival process at a M/M/m queueing system with infinite queue capacity have
parameter  .
Then, under steady-state conditions (i.e., for .
Then, under steady-state conditions (i.e., for  < m < m ), the departure process from the queueing
system is also Poisson with parameter ), the departure process from the queueing
system is also Poisson with parameter  . .
The proof of this property is quite involved.
However, it is relatively straightforward for the special case M/M/1 (see Problem 4.10).
The implications of the property for the
analysis of queueing networks are quite obvious. If some "component" (facility)
of a queueing network can be modeled as a M/M/m system with infinite capacity, the
"output" of this "component" is also Poisson with parameter  . That is, users
will leave this specific facility according to a probability distribution identical to the
probability distribution for the arrival of users at the facility. . That is, users
will leave this specific facility according to a probability distribution identical to the
probability distribution for the arrival of users at the facility.
Thus, if the served users of the M/M/m facility
are subsequently routed to another facility, the arrival process to this other facility is
a Poisson process. In fact, it is clear that if
1. the queueing network consists of, say, K facilities in series (Figure
4.17), each of which
contains m1,
m2, . . . , mk (mi
= 1, 2, 3, ...) identical servers with negative exponential
service and rates  i, (i =1, 2, . . .
, K); i, (i =1, 2, . . .
, K);
2. there is infinite queueing space between successive facilities; and
3. the arrival process for the first facility (facility 1 in Figure
4.17) is Poisson with rate  ; ;
then, under steady-state conditions, the queueing network can be analyzed as K
independent M/M/m queues and the results of Section 4.6 are directly
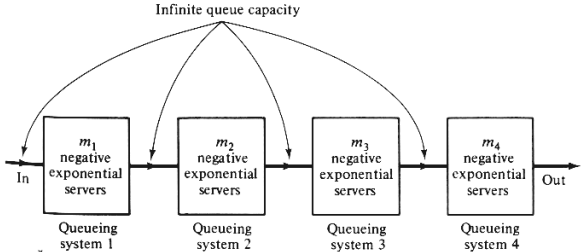
FIGURE 4.17 Poisson input at rate  at
queueing system 1 will result in a Poisson input at rate at
queueing system 1 will result in a Poisson input at rate  for all
four queueing systems. for all
four queueing systems.
applicable. The condition for steady state in this case is that  < mi < mi i, for all
i(i = 1, 2, . . . , K). i, for all
i(i = 1, 2, . . . , K).
Three additional notes:
1. It is not necessary that all users proceed in series from one facility
to the next. For instance, in a "feedforward" network (i.e. a network without
any feedback loops) of the type shown in Figure 4.18, departing users from a facility may
be divided among N subsequent facilities according to the probabilities pj
(j = 1, 2, . . . , N; 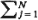 pj=1. Here pj
represents the probability that a user departing the facility will go to facility j, with
the routing of each user determined independently. Since the streams of events that result
from the subdivision (in the way described above) or from the mixing together of Poisson
streams are also Poisson, the M/M/m analysis can also be used in such, more complicated
cases.14 Thus, as an example for the network shown in Figure
4.18, all flows between facilities are Poisson as long as the arrival processes
represented by pj=1. Here pj
represents the probability that a user departing the facility will go to facility j, with
the routing of each user determined independently. Since the streams of events that result
from the subdivision (in the way described above) or from the mixing together of Poisson
streams are also Poisson, the M/M/m analysis can also be used in such, more complicated
cases.14 Thus, as an example for the network shown in Figure
4.18, all flows between facilities are Poisson as long as the arrival processes
represented by  1, 1,  2, and 2, and  3,
are Poisson and as long as the assumptions in the equivalence property hold for each
queueing system separately. 3,
are Poisson and as long as the assumptions in the equivalence property hold for each
queueing system separately.
2. The equivalence property does not hold for the case of M/M/m
queueing systems with finite queue capacity. It is simple using a state-transition diagram
to argue intuitively why this is so. Queueing networks composed of M/M/m queues of this
type are often analyzed using the state-transition diagram approach that we shall describe
below.
3. Unfortunately, the "negative" statement of the equivalence
property is also true: it can be shown [GROS 74] that the only type of service
distribution which results in a Poisson output, if the input to the queueing system is
Poisson, is the negative exponential distribution. Thus, a necessary condition for the
output (the departure process) of a M/G/m queueing system to be Poisson is that "G =
M" (i.e., that the service time distribution be negative exponential). The only
exception to this rule is the M/G/ queueing system. As a result of this negative side of the
equivalence property, the presence in a queueing system of even a single facility with
service times that are not negative exponential often creates serious analytical problems.
15 queueing system. As a result of this negative side of the
equivalence property, the presence in a queueing system of even a single facility with
service times that are not negative exponential often creates serious analytical problems.
15
15 For practical purposes, however, the output of a M/G/m queueing system can
often be assumed approximately Poisson for large m. This is true due to a limit theorem
stating that, when a large number of renewal processes are pooled together, the resulting
process approaches Poisson, irrespective of the type of the individual renewal processes.
14 The reader should be aware that many "subtleties" arise in the
analysis not only of queueing networks that permit some types of feedback but also of some
types of feedforward networks (see [KLEI 75] [KLEI 76] and, especially, [DISN 79]). For
instance, in networks with feedback, the flow of units within the network may not be
Poisson.
|