4.8.4 G/G/m Queueing Systems
About the only general results
that have been
obtained to date for the G/G/m case are in the form of quite loose
upper and lower bounds
on average steady-state queueing characteristics. [BRUM 71]. These
bounds are often
computed by, first, comparing a G/G/m system with a G/G/1 system
that has the same
"service potential" as the G/G/m system (i.e., the single
server in G/G/1 works
m times as fast as each of the servers in G/G/m) and, then, by using
the earlier results
on G/G/1.
The best generally
applicable bounds on the
average waiting time in queue which have been published to date for
G/G/m systems give the
inequalities
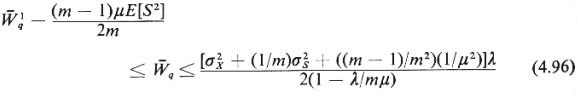
where  , , 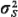 , and E[S , and E[S ] are the
service rate, variance of service time, and s second moment of
service time, respectively,
for each of the m servers. ] are the
service rate, variance of service time, and s second moment of
service time, respectively,
for each of the m servers. 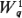 is the average waiting time for a G/G/1
system with a service
time described by a random variable S* = S/m (i.e., with
service m times
faster than that of each of the m servers in the G/G/m system) and
with an arrival process
identical to that for the G/G/m system. is the average waiting time for a G/G/1
system with a service
time described by a random variable S* = S/m (i.e., with
service m times
faster than that of each of the m servers in the G/G/m system) and
with an arrival process
identical to that for the G/G/m system.
For 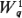 , one should obviously use either an
exact expression, if one
is available, or, as is more likely, a lower bound on , one should obviously use either an
exact expression, if one
is available, or, as is more likely, a lower bound on 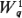 by using (4.92) or, if
applicable, (4.94). For
example, for the M/G/m queueing system, one should use the exact
expression (4.81) for by using (4.92) or, if
applicable, (4.94). For
example, for the M/G/m queueing system, one should use the exact
expression (4.81) for 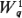 with 1/m
with 1/m and
and
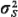 /m /m , for the
expected value and variance of the service times, respectively. , for the
expected value and variance of the service times, respectively.
Finally, a result
analogous to the
heavy-traffic approximation for G/G/1 systems has also been
derived recently [K0LI,
74] for G/G/m systems. This result states:
For  m m
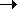 1 in a G/G/m
system, the waiting time in queue under steady-state conditions
assumes a distribution
that is approximately negative exponential with mean value 1 in a G/G/m
system, the waiting time in queue under steady-state conditions
assumes a distribution
that is approximately negative exponential with mean value
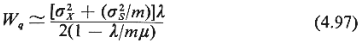
Note once more that
expected waiting time is
dominated by a (1 - 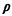 ) )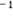 term, as term, as 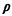 approaches 1 ( approaches 1 (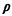 = =  /m /m for multiserver systems). for multiserver systems).
|