4.9.1 Prememptive and Nonpreemptive Priorities
Priorities that differentiate among classes of
users are generally classified as preemptive or nonpreemptive. In either case, as soon as
service to any particular user has been completed, the system chooses as the next user a
representative of the highest-priority class present. (Priorities within classes
are determined according to FCFS, LCFS, SIRO, or some other discipline.)
The difference, however, lies in the fact that in systems using preemptive priorities,
high-priority users are never kept waiting in favor of lower-priority ones. That is, the
system stands ready to interrupt service to any present occupant of the service facility,
immediately upon arrival of a user belonging to a class with higher priority than that of
the present facility occupant. By contrast, nonpreemptive systems never interrupt a
service to a user once that service has begun-even if a higher-priority user arrives at
the system while this service is going on.
For preemptive systems, what happens to users
who get "ejected" from the service facility is in itself a matter to be
specified. In some systems, service to the ejected user-once that user eventually regains
hold of the service facility-continues right from the point where it was interrupted. In
other systems, service may have to be restarted from scratch. (Note that for users whose
service times are negative exponential, these two cases are indistinguishable.) It is also
conceivable that an ejected user may be assigned to a priority class higher than his
former one, in compensation for being ejected.
It should also be noted that many queueing
systems-especially in the urban environment-operate with different priority rules for
different user classes. For instance, it is possible that users in a class with very
high-priority status may obtain preemptive service, whereas users of medium importance may
enjoy only nonpreemptive priority over users in the low-priority classes. Such is the case
in police dispatching where an incident reporting "a police officer in danger"
is almost always accorded preemptive priority, while other types of high-priority
incidents may be nonpreemptive. Finally, it is also possible that different queue
disciplines (e.g., FCFS, SIRO, etc.) may be used within
different classes of users at the same queueing system. Thus, users who belong to, say,
class A may queue up according to a FCFS order, whereas users in another
class, B, may be served in random order.
If nothing else, it should be clear from the
above that there exist a bewildering number of variations of queueing systems with class
priorities. Of those variations, queueing theorists have studied with some success a few
and have derived an interesting (but hardly exhaustive) set of results. We shall review
now some of the most important and useful of those results, always with reference to the
type of queueing model shown in Figure 4.15. Facility users in this model are separated
into a number, say r, of distinct user classes. Each class is assigned a priority number k,
k = 1, 2, . . . , r, for use of the service facility. By convention, the smaller
the priority number, the higher the priority of the class.
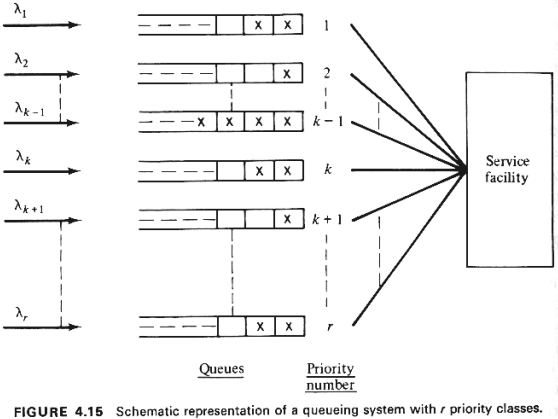
Each of the r queues will be assumed to run on
a FCFS basis, but any given priority class cannot obtain access to the
service facility unless no other user belonging to a higher-priority (lower-k) class is
present in the queues. However, whether user service is ever interrupted or not will
depend on whether the queueing system uses preemptive or nonpreemptive priorities.
Finally, we note at the outset that in all
cases that will be examined in this section, it is assumed that arrivals for each
priority class are Poisson with arrival rate 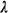 k for priority
class k. k for priority
class k.
Nonpreemptive priorities in a M/G/1 system. We shall consider
first the case in which the queueing model of Figure 4.15 contains a single server that
operates under a nonpreemptive priority regime. Moreover, we shall assume that the random
variable Sk, which describes the service time for
users in priority class k, has a general probability density function, expected
value
1/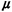 k,
and second moment E[S k,
and second moment E[S k]. We shall also define the
quantity k]. We shall also define the
quantity 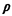 k
- k
-  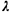 k/ k/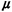 k.
Thus, the queueing system of Figure 4.15 is a M/G/1 system with utilization ratio given by k.
Thus, the queueing system of Figure 4.15 is a M/G/1 system with utilization ratio given by
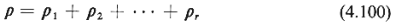
The system queueing capacity is assumed to be infinite.
Under these assumptions, we shall now proceed
to derive an expression for the average waiting time in queue for a user in priority class
k, 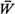 qk.
To do this, let us consider the arrival of a random user from class k at the queueing qk.
To do this, let us consider the arrival of a random user from class k at the queueing
system. We can immediately write an expression for 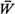 qk (in steady
state) as follows: qk (in steady
state) as follows:
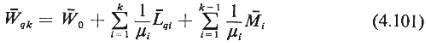
where 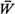 0 = expected remaining
time in service for the user who occupies the server at the time when the new user (from
class k) arrives at the queueing system 0 = expected remaining
time in service for the user who occupies the server at the time when the new user (from
class k) arrives at the queueing system
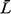 qi
= expected number of users in priority class i who are already waiting in queue at the
instant when the new user
(from class k) arrives qi
= expected number of users in priority class i who are already waiting in queue at the
instant when the new user
(from class k) arrives
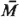 i =
expected number of users in priority class i who will arrive while the newly arrived user
(from class k) waits in
the queue i =
expected number of users in priority class i who will arrive while the newly arrived user
(from class k) waits in
the queue
To comprehend the meaning of (4.101) it is
important to notice that the first summation on the right includes user classes 1 through
k (including k) since users from these classes who are already waiting when our
new user arrives at the system will be served before the new user. By contrast the new
user takes precedence over all users of classes k + 1, k + 2, . . . , r who are already
waiting. Therefore, these classes do not affect the expected waiting time of the new user
and thus do not appear in (4.101). Note also that the second summation is for classes 1
through k -1 (does not include k) since users from these classes who arrive while our new
user from class k is waiting will take precedence over the user from class k.
We now set out to evaluate the quantities 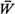 0, 0, 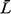 qi,
and qi,
and 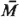 i
(4.101). i
(4.101).
Beginning with 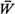 0, note that if the
server at the instant of the new user's arrival is occupied by a user from priority class
i, we have [see our discussion of random incidence in Chapter 2 and, in particular,
(2.66)] 0, note that if the
server at the instant of the new user's arrival is occupied by a user from priority class
i, we have [see our discussion of random incidence in Chapter 2 and, in particular,
(2.66)]
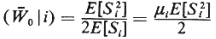
But since we have Poisson arrivals for users of class k, the probability
that a user of class i will be occupying the server at the instant of our random arrival
is simply equal to the fraction of time, pi, that users of type i
occupy the server. Thus,
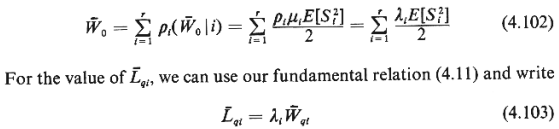
(Note that the 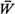 qi are still unknown.) Finally, for
the expected number of users of class i, qi are still unknown.) Finally, for
the expected number of users of class i, 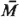 i, who arrive during the
time when the new user from class k is waiting in line, it is clear that since the
arrival process for type i users is Poisson with rate i, who arrive during the
time when the new user from class k is waiting in line, it is clear that since the
arrival process for type i users is Poisson with rate 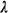 i, i,

and 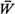 0, is as given by
(4.102). 0, is as given by
(4.102).
Expression (4.107) is probably the best-known
result in the literature on queueing systems with priorities. From it and through use of
(4.11), (4.10), and (4.13), one can obtain expressions for 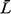 qk, qk, 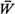 k,
and k,
and 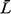 k,
for all classes of users k. users k. It should also be emphasized that (4.107)
demonstrates clearly the fact that in a nonpreemptive priority system, steady state may be
reached for some priority classes and not for others. From (4.107), priority class k
will reach steady state as long as ak < 1,
since for that condition k,
for all classes of users k. users k. It should also be emphasized that (4.107)
demonstrates clearly the fact that in a nonpreemptive priority system, steady state may be
reached for some priority classes and not for others. From (4.107), priority class k
will reach steady state as long as ak < 1,
since for that condition 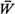 qk is positive and finite. That is,
if there is an integer p (1 qk is positive and finite. That is,
if there is an integer p (1  p p r) such that r) such that 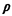 1, + 1, + 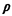 2
+ ... + 2
+ ... +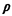 p
+ p
+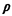 p+1 p+1
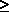 1, then the p
highest priority classes reach steady-state delays while users in classes p + 1
through r experience unbounded waiting times. In this case, (4.107) must be modified
slightly to account for the fact that, in steady state, priority classes 1
through p occupy the server for a fraction of time equal to 1, then the p
highest priority classes reach steady-state delays while users in classes p + 1
through r experience unbounded waiting times. In this case, (4.107) must be modified
slightly to account for the fact that, in steady state, priority classes 1
through p occupy the server for a fraction of time equal to 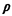 k each (k = 1, 2, . . . ,
p); class p + 1 occupies the server for a fraction of time equal to 1 - ap;
and, finally, classes p + 2 through r do not ever obtain access to the server. We
then have k each (k = 1, 2, . . . ,
p); class p + 1 occupies the server for a fraction of time equal to 1 - ap;
and, finally, classes p + 2 through r do not ever obtain access to the server. We
then have
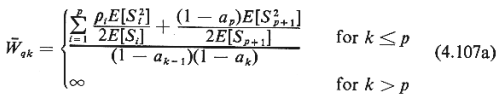
Note that (4.107a) reduces to (4.107) for p = r. Note also that the Wqk
do not depend on users in priority classes lower than k, except for the
contribution of these users to the numerator of (4.107) or of (4.107a).
11 In the expression for 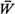 q1, we must set a0
= 0. q1, we must set a0
= 0.
|