4.9.4 Preemptive Priorities
Some results also exist for the case of systems
with preemptive priorities, both for the preemptive-resume and the preemptive-repeat
types. The former refers to the situation in which service to an ejected user, once that
user regains access to a server, continues from the point where it was interrupted
earlier. By contrast, in the latter type of preemptive system, all service received
already is "lost" once a user is ejected from service prior to service
completion.
The one result that will be presented here for
the preemptive case once again fits the model of Figure 4.15 with a single server.
However, it is now assumed that the service time distribution is negative exponential and,
in addition, that all classes of users have the same expected service rate  . As we have noted
already, the preemptive resume and the preemptive repeat cases are now identical because
of the lack of memory of the server. . As we have noted
already, the preemptive resume and the preemptive repeat cases are now identical because
of the lack of memory of the server.
For this model it can be shown (see, e.g.,
[KLEI 76]) that
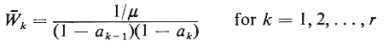 (4.113) (4.113)
where  k, as usual, signifies
the total expected system time13 for a user in class k and,
as in the previous section, ak = k, as usual, signifies
the total expected system time13 for a user in class k and,
as in the previous section, ak = 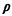 1
+ 1
+ 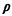 2
+ ... + 2
+ ... + 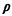 k.
More results for preemptive priority systems are derived in Problem 4.9. k.
More results for preemptive priority systems are derived in Problem 4.9.
Example 2: Repair Work with Priorities
Consider a repair crew charged with performing work for vehicles of the local urban
transit authority. Vehicles are separated into two types and break downs occur in a
Poisson manner at rates of  1, and 1, and  2
for the two types of vehicles, respectively. Repair times are negative exponential and the
average service time is the same, 1/ 2
for the two types of vehicles, respectively. Repair times are negative exponential and the
average service time is the same, 1/ , for both types. Assuming that , for both types. Assuming that
 1
+ 1
+  2
< 2
<  , we wish to
compare the expected system occupancy time (time spent waiting for repair plus time under
repair) for each type of vehicle for: , we wish to
compare the expected system occupancy time (time spent waiting for repair plus time under
repair) for each type of vehicle for:
1. The case where type 1 vehicles enjoy
preemptive priority over type 2 vehicles.
2. The case where type 1 vehicles enjoy
nonpreemptive priority over type 2 vehicles.
3. The case where no priorities exist and
breakdowns are repaired in a FCFS fashion, irrespective of the type of vehicle.
Solution

Furthermore,
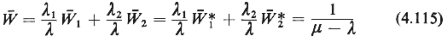
That is, the average system occupancy time for all breakdowns is identical for the three
cases. The relationship shown in (4.115) is a simple example of what are often referred to
in queueing theory as "conservation relations." A more general result along
these lines and some interesting related questions are developed in [KLEI 76].
13 Note that (4.107) and (4.111) refer to expected waiting
time.
|