4.14 Police helicopters and police cars Assume that in a
circular city with a
radius of R miles, calls for police service are generated in a
Poisson manner at the rate
of 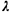 per
hour per city square mile. Calls are uniformly distributed over the
city. per
hour per city square mile. Calls are uniformly distributed over the
city.
The police department is
contemplating the
purchase of k helicopters to respond to certain types of
police calls. The
helicopters will be flying straight to the location of each
incident, at an effective
speed of
vH,
miles/hr.
The special police cars
that are presently used
for these calls have an effective speed of
vc,
miles/hr and travel in right- angle distances. The city is rather
large and its streets
have no particular orientation with respect to the coordinate axes.
The dispatching
strategy that the police
controller uses, whether operating a helicopter-based or a car-based
system, is the
following. Whenever all service units are busy, calls for police
assistance are placed in
a first-come, first-served, infinite capacity queue and the first
service unit which
becomes available is immediately dispatched to the first call in the
queue. If, on the
other hand, more than one service unit is available, the dispatcher
selects one of the
available units randomly (with no consideration to service
unit locations) and
dispatches it to the next call.
It is also known that the
durations of service
for incidents serviced by helicopters or by cars, after
arrival on the scene, are
random variables with negative exponential distributions with
average service time equal
to 1/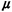 H
and 1/ H
and 1/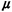 c,
respectively. The durations of service to successive incidents are
statistically
independent. c,
respectively. The durations of service to successive incidents are
statistically
independent.
Finally, it is known that
a unit that completes
service to a call remains stationary until it is dispatched to a new
incident.
a. Make the assumption that travel times to successive
incidents for any given
service unit are statistically independent. Also assume
steady-state conditions.
Let the
criterion for comparison
between the k helicopter system and the m police car
system be that fraction of
time that a randomly selected service unit is busy (a server is
considered busy if it is
either traveling to the scene of an incident or servicing a call
at the scene). Find the
value of m for which the car-based system will most
closely match the helicopter
system for any given number k of helicopters.
Your answer
should be an expression
for m containing only variables defined above and constants.
Please explain your work.
b. For R = 4,
vH = 80
mph, vc = 25 mph, and 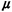 H
= H
= 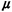 c,
= 4 calls per hour, compute the ratio m/k for your answer
in part (a). c,
= 4 calls per hour, compute the ratio m/k for your answer
in part (a).
c. In part (a), we assume that travel times to successive
incidents for any given
service unit are statistically independent.
Is this assumption a
correct one? Please
explain briefly and clearly in intuitive terms.
d. Assume now that there are two helicopters (and no police
cars in the district). Also
assume that R/vH
<<
1/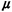 H.
Find a good approximation for the probability that, with the
system in the steady state,
an observer arriving at a random instant will find both
helicopters busy and exactly one
call waiting in the queue. For what condition is your answer true? H.
Find a good approximation for the probability that, with the
system in the steady state,
an observer arriving at a random instant will find both
helicopters busy and exactly one
call waiting in the queue. For what condition is your answer true?
e. Under the assumptions of part (d), find the probability that
with the system in the
steady state, the two helicopters will complete service to exactly
l
calls during a time interval T.
|