4.16 M/Hk/m queueing systems
The hyperexponential
pdf of order k is the pdf
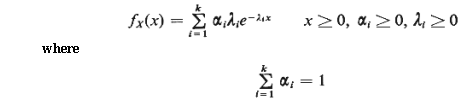
In other words, a
hyperexponential pdf can be
viewed as the weighted sum of k distict negative
exponential pdf's.
a. Show that, for the random variable X with hyperexponential
pdf,
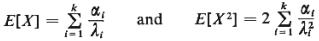
b. Show that the coefficient of variation of X,
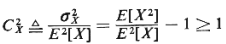
Hint: Use the Cauchy-Schawrz inequality,
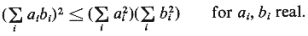
Because of the fact
that C x x 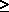 1, hyperexponential
random variables are said to be "more random" than
negative exponential random
variables (for which C
1, hyperexponential
random variables are said to be "more random" than
negative exponential random
variables (for which C =1). =1).
c. Consider now a
M/H2/1 queueing system with
infinite queue capacity
(H2 indicates that
service times are
second-order hyperexponential random variables.) Let 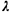 = 3 be the
arrival rate at the system
and let the service time pdf be given by = 3 be the
arrival rate at the system
and let the service time pdf be given by
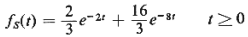
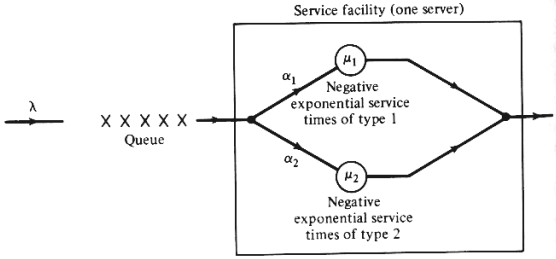
A schematic
representation of this system is
shown in Figure P4.16. Each user, upon entrance to the service
facility, will receive type
1 service with probability  1 or
type 1 or
type  2
service with probability 2
service with probability  2.
Whenever either one of the two types of services is being
offered, no other user
can obtain access to the facility. What are the values of 2.
Whenever either one of the two types of services is being
offered, no other user
can obtain access to the facility. What are the values of  1, 1,
 2, 2,
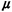 1,
and 1,
and 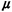 2
in this case? 2
in this case?
d. Find 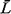 , ,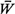 , ,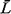 q and q and 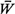 q in this
case. Compare with the equivalent quantities for a M/M/1 system
with service rate (when
busy) equal to the service rate of this
M/H2/1
facility. q in this
case. Compare with the equivalent quantities for a M/M/1 system
with service rate (when
busy) equal to the service rate of this
M/H2/1
facility.
e. Carefully draw a state-transition diagram for
this M/H2/1
system.
Hint 1: Define states: "0" = the system
is empty; "i,j"=
i users are present (i=1,2, ...) and the user
currently occupying the
service facility is receiving type j
service (j =
1,2).
Hint 2: The rate of transitions from state 0 to
state (1,1) is equal to  1 1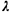 ; the rate of
transitions from state (2,2) to state (1,1) is equal to ; the rate of
transitions from state (2,2) to state (1,1) is equal to  1 1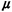 2. 2.
f. Describe a possible situation in an urban
service system context
whereM/Hk/1 (or
M/Hk/m) models could
be applicable.
|