


5.3.5 Facility LocationLarson and Stevenson, in work concurrent with that of Carter, Chaiken, and Ignall, used a particular form of the two-server model to examine certain questions of optimal facility location [LARS 72]. In particular, they considered an n x m rectangular region in which service requests are uniformly distributed and in which facility 1 is located at (x1, y1). One is free to position facility 2 at any location (x2,y2) and to construct optimal response areas. This situation might correspond to one in which an existing facility serving the region is overburdened and a second facility is about to be introduced. The problem is to locate the second facility and to partition the region so that the resulting mean travel time is minimized. A similar type of problem in a network context is related to the "p-median" problem (see Chapter 6). Travel time is assumed to be right-angle, with directions of travel parallel to the sides of the rectangle. As one varies so a first question involves the change of the candidate boundary lines. Applying the Carter-Chaiken-lgnall result in this case, an optimal boundary consists of points (x, y) satisfying an equation of the form where (x1, y1 ) and (x2, y2 ) are the respective facility coordinates. Equation (5.19) generates the family of boundaries, either type 1 or type 2, illustrated in Figure 5.3. For any given (x1, y1 ) and(x2, y2 ), it turns out there will be two values for so which do not yield unique boundaries but rather regions in which all points are so closer to one facility than to another. Any line partitioning B and contained in such a region is an optimal boundary.
The system's mean travel time, while containing many terms, can be found almost by inspection by repeated application of the ideas in Sections 3.4.1 and 3.8, linking pdf's to geometric designs of service regions. For instance, for a very low utilization system, in which the frequency of interresponse area dispatches is negligibly small, the optimal boundary is the equal-travel-time boundary (i.e., so = 0). For this case, suppose that facility 2 is located north to northeast of facility 1: 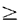 x1 x1y2 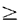 y1 y1y2 - y1 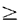 x2 - x1
x2 - x1
yielding a type 1 boundary (see Figure 5.3). Then, by repeated conditioning on rectangular and triangular subregions one obtains, for the mean systemwide travel time,
For each of the other seven possibilities for the relative placement
of facilities, the expressions for For the case of To indicate the qualitative properties of the results, we discuss as an example a region for which n = 1, m = 2. We continuously vary the position of facility 1 over a closed trajectory in the southern half of the region. We then examine the locus of optimal positions of facility 2 induced by varying facility 1 over the fixed trajectory. In Figure 5.4 we see the effect of varying the position of facility 1 over a circular trajectory centered at (0.5, 0.5) and having radius 0.45. The most striking feature of Figure 5.4 is that for large changes in the position offacility 1, the change in the position of facility 2 to maintain optimality is relatively small.
On occasion, a continuous trajectory of facility 1 locations induces a discontinuous trajectory of optimal facility 2 locations, the discontinuities occurring at points where the optimal boundary configuration changes, say, from type 1 to type 2. The mean travel time is found to be continuous, however. This effect is seen clearly in Figure 5.5, in which the position of facility 1 is varied over a square centered at (0.5, 0.5) of dimension 0.9, yielding a dis continuous trajectory of optimal facility 2 locations. We see that, for facility 1 near the top corners of the square, the optimal location of facility 2 jumps to a region in which a type 2 (rather than a type 1) boundary is required.
Corresponding to the two trajectories for facility 1 in Figure 5.4
and 5.5, we have plotted in Figure 5.6 the mean travel time
We may now be interested in how the optimal trajectory for facility 2
changes as
For
These last two observations are more pronounced for Following the method illustrated above, we plot in Figure 5.9 the
minimal mean travel time 3Because of the symmetry of facility 1 locations about x = 0.5, we have graphed |