We state explicitly below the nine key assumptions underlying the
basic hypercube queueing model that we will develop in the subsequent
section. Successful generalizations of this basic model have allowed
modifications to assumptions 6, 7, and 9 [LARS 74a, 75b, 78, 80; JARV
74; HALP 77; CHEL 80].
- Geographical atoms
. The area in which the system provides
service can be broken down into a number NA of
"statistical reporting areas" or "geographical atoms." These might
correspond, for instance, to census blocks, small collections of city
blocks, or police reporting areas. In the model each atom is modeled
as a single point, located near the center of the actual atom.
- Independent Poisson arrivals
. Requests for service
("customers") are generated as a Poisson process, independently from
each of the atoms. The Poisson arrival rate 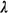 j, from atom j (j =
1, 2, . . ., NA) is known or can be estimated.
j, from atom j (j =
1, 2, . . ., NA) is known or can be estimated.
- Travel times
. Data are available to estimate the mean
travel time 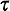 ij from each atom
i to each atom j (i, j = 1, 2, . . .,
NA). In the absence of such data, plausible
approximations for travel times can be made using geometical probability
concepts (perhaps employing the Manhattan or Euclidean distance metric
or an empirical time-distance relationship).
ij from each atom
i to each atom j (i, j = 1, 2, . . .,
NA). In the absence of such data, plausible
approximations for travel times can be made using geometical probability
concepts (perhaps employing the Manhattan or Euclidean distance metric
or an empirical time-distance relationship).
- Servers.
There are N spatially distributed servers,
or response units, each of which can travel to any of the geographical
atoms in the serviced region.
- Server locations.
The location of each response unit,
while not servicing a customer, is known (at least statistically). For
instance, a patrolling police car may allocate 50 percent of its patrol
time in atom 12 and 25 percent each in atoms 8 and 11. A fixed position
unit, such as an ambulance or delivery truck, would always be located in
one particular atom (except when providing service). For
non-fixed-position units, the set of atoms in which the unit may be
located while available for assignment is called the unit's patrol area.
In police applications patrol areas are usually called "beats,"
"sectors," or "routes." In general, patrol areas may overlap.
- Server assignment.
In response to each request for
service, exactly one6 response unit is dispatched to
the scene of the request, provided that at least one unit is available
within the service region. If no unit is available, the request either
enters a queue with other backlogged requests, or it is lost, or it is
serviced by some backup system (e.g., police providing backup to an
ambulance service or a neighboring community dispatching units into the
temporarily saturated community). If the request enters a queue, it is
later dispatched according to a queue discipline that does not depend on
anticipated service time or geographical location of the request;
allowable disciplines are, for instance, first-come, first-served;
last-come, first-served; and random. Upon completion of service, a
service unit either is dispatched to a request waiting in queue or it
immediately returns to its home location.
6The assumption of dispatching exactly one unit to a request
indicates that the model.
- Fixed-preference dispatching.
Server assignment takes
place according to a fixed-preference procedure. By this we mean the
following. Suppose that a request for service arrives from atom 12. Then
there is an ordered list of units, say (3, 1, 7, 5, 6, 4, 2) for a
seven-unit problem, that specifies the dispatcher's preference for units
to assign to atom 12. The possibility of ties in preference is, for
convenience, excluded from our discussion here. The dispatcher starts
with the first entry in the list, unit 3 in this case, and assigns that
unit, if available. Here atom 12 is in unit 3's primary response
area.7 If the first preferred unit is not available, then
the dispatcher assigns, if available, the first backup unit (the second
preferred unit), which is unit 1 in this case. The dispatcher continues
down the list until the first available unit is found (if there is one),
and assigns that unit. This procedure is called a "fixed-preference"
procedure since the ordered list of preferences does not change with the
state of the system. However, the list of preferences may change by
atoms, as for instance, the list for atom i + 1 may be (5, 6, 3,
1, 7, 2, 4). The model can operate with any fixed-preference dispatch
policy. With NA atoms and N response units,
there are (N!)NA possible different
dispatch policies.8
7A unit's primary response area consists of that set of
geographical atoms to which it would be assigned first if it were
available. A primary response area may or may not coincide with a unit's
patrol area (for the case of non-fixed-position units). For any
particular unit, there may be no atoms in its primary response area.
However, each atom must be contained in one (and only one) primary
response area. Examples of primary response areas are ambulance zones,
police beats, and service areas.
8If we include the possibility of ties in dispatch
preference (which is excluded from our discussion here), the number of
different policies becomes even more enormous.
- Service times.
The service time for a request, including
travel time, on-scene time, and possible related follow-up time, has a
known average value. In general, each response unit may have its own
average service time. Moreover, reflecting the unpredictability of
service times in actual systems, there is considerable variation about
the average value(s). As one measure of the variability, the standard
deviation of the service time is assumed to be approximately equal to
the mean. The mathematical analysis assumes negative exponential service
times, but reasonable deviations from this assumption have been found
not to alter in any practical way the predictive accuracy of the model.
- Service-time dependence on travel time.
Variations in the
service time that are due solely to variations in travel time are
assumed to be second order compared to variations of on-scene and
related followup service time. This assumption, which limits the
applicability of the model, is most nearly satisfied by urban police
departments, emergency repair services, and some home visit social
service agencies, and least nearly satisfied by rural emergency services
(especially rural ambulance services). As explained earlier in the
chapter, this assumption does not imply that travel time is ignored in
computing mean service time; through the process of mean service-time
calibration, the mean service time 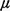 n-1 for server n
is equal to the sum of the mean travel time for that server, the mean
on-scene time, and the mean off-scene follow-up time.
n-1 for server n
is equal to the sum of the mean travel time for that server, the mean
on-scene time, and the mean off-scene follow-up time.
In practice, no actual service system will ever conform exactly to
all the model's assumptions. In applying the model, one must weigh the
extent to which the actual system does not fit the rigidities of the
model (and the associated loss in predictive accuracy) against
alternative methods (with their own limitations) to choose that method
which best suits the decision-making goals at hand.
Given the foregoing assumptions, the model computes numerical values
for the following performance measures:
- Region-wide.
Mean travel time, average workload and
workload imbalance, fraction of assignments outside a unit's primary
response area.
- Response-unit-specific
. Workload (measured in fraction of
time busy servicing requests), mean travel time, fraction of responses
outside the unit's primary response area.
- Primary-response-area-specific.
Internally generated
workload (which is an input measure), mean travel time, fraction of
requests serviced by other than the primary response unit.
- Atom-specific.
Internally generated workload (which again
is an input measure), mean travel time, fraction of requests serviced by
each unit n (n = 1, 2, . . ., N).
In addition, if the service being modeled is a police patrol force,
one can calculate the frequency of patrol vehicle passings in each of
the geographical atoms.


