


5.6 FRACTION OF DISPATCHES THAT ARE INTERRESPONSE AREA DISPATCHES
Often an agency administrator will want to know the number of dispatches that take units outside of their primary response areas. Such responses increase travel time and they may result in degraded service due to unfamiliarity with the neighborhood (its geography, people, and traditions). While we could compute this quantity exactly with the hypercube model, it is instructive to obtain some approximate "back-of-the-envelope" results for situations with many servers N. In particular, we wish to see how the number of interresponse area dispatches varies with average system-wide workload, workload imbalances, and time-varying demands for service. For a given region with many response units N, define
Given a request that arrives from primary response area n, we assume hat the dispatching strategy is as follows:
Invoking a large-N (or low-workload) assumption, we assume that the probability that all units are simultaneously busy is negligibly small. Suppose that a service request arrives from response area n at
time t. The probability that it will result in an interservice
area dispatch is equal to the probability that unit n is busy
[i.e., 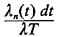
Thus, the likelihood that a random request arrives in t to t + dt, is from response area n, and results in an interresponse area dispatch is  n(t) n(t)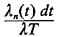
Summing over all N response areas and integrating over [0, T] we obtain the probability that a random dispatch that occurs in [0, T] will be an interesponse area dispatch,
If the system is non-time-varying, with
In Problem 5.14 we explore some special cases of (5.56). We will find, in general, that fI increases as workload imbalances increase. If workloads are fairly well balanced, one can often approximate fI to equal (or slightly exceed) the average fraction of time units are busy, averaged over all units, provided that the system is non-time-varying. What if the system is time-varying? We can show that this usually
"makes things worse," assuming that interresponse area dispatches are
undesirable. That is, given one further assumption, we can obtain a
bound for fI in a time-varying system which states
that the amount of interresponse area dispatching is at least as great
as that which would occur in the "equivalent" non-time-varying system.
To describe this equivalent system, we simply replace 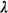 n = n = 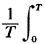 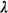 n(t) dt n(t) dt n = n = 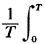  n(t) dt n(t) dt
The additional assumption we require is that We wish to prove, given the foregoing assumptions, that fI for the time-varying system as computed from (5.55) satisfies the following inequality:
Proof: Let  n(t) = n(t) =  n + n + 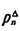 (t) (t)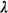 n(t) = n(t) = 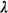 n + n + 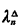 (t) (t)
Clearly, the perturbation terms on the right-hand side integrate to zero; that is, 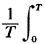 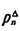 (t) dt = 0 (t) dt = 0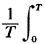 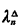 (t) dt = 0 (t) dt = 0
From (5.55) we have 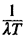 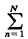 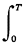 [ [ n n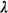 n + n +  n n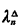 (t) + (t) + 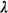 n n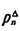 (t) + (t) + 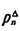 (t) (t)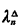 (t)]
dt (t)]
dt
Since the second and third terms in the integrand integrate to zero, 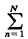  n n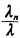 + + 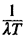 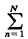 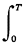 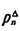 (t) (t)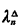 (t) dt (t) dt
Now, since 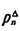 (t)] = sgn [ (t)] = sgn [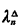 (t)] (t)]
then 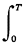 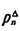 (t) (t)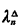 (t)
dt (t)
dt 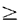 0 0
and thus (5.57) must be true. Problem 5.14 asks you to reexamine this analysis for systems that do not always give first preference to the primary response area's unit (e.g., a system incorporating an automatic vehicle locator system, which would allow the dispatcher to assign the vehicle closest to the scene of the service request). |