|
5.12 Fire problem Consider three fire stations, A,
B, and C, located on the X-axis at -1, 0, and +1,
respectively. The fire trucks at these stations service fires that are
reported in the region X = -2 to X = +2. Fires within this
region are independently uniformly distributed; they are generated at
the rate 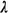 per hour. Travel time to and from
the fires is instantaneous. Service time at the scene is negatively
exponentially distributed with mean 1/ per hour. Travel time to and from
the fires is instantaneous. Service time at the scene is negatively
exponentially distributed with mean 1/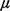 . There is
one truck at each station and the dispatcher will assign the closest
available truck. If no truck is available, reports of fires enter a
queue that is depleted in a first-come, first-served manner. . There is
one truck at each station and the dispatcher will assign the closest
available truck. If no truck is available, reports of fires enter a
queue that is depleted in a first-come, first-served manner.
- Write down the equations whose solution would provide the
utilization factor (fraction of time busy) of each of the trucks. You
need not solve the equations.
- Write down the equations whose solution would provide the
fraction of calls generated in the interval X = -½to X
= +½ that are serviced by unit C. You need not solve the
equations.
- Find approximate solutions to parts (a) and (b) by
employing the hypercube approximation procedure of Section 5.5 and
Problem 5.11.
|


