


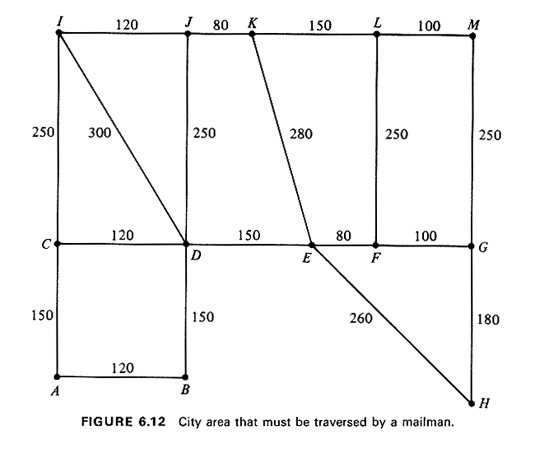
6.4.1 Edge Covering: The Chinese Postman's ProblemConsider the case of a mailman who is responsible for the delivery of mail in the city area shown in graph form on Figure 6.12. The mailman must always begin his delivery route at node A where the post office.is located; must traverse every single street in his area; and, eventually, must return to node A (while using only the street grid shown). The lengths of the edges of the graph (where each edge represents a street segment between street intersections indicated as nodes) are given on Figure 6.12. The graph is undirected. The most natural question to ask in this case is: How should the mailman's route be designed to minimize the total distance he walks, while at the same time traversing every street segment at least once10 This type of edge-covering problem is known as the Chinese postman's
problem
We shall discuss the problem only for undirected graphs and we
use Problem 6.6 to extend our results to directed graphs.
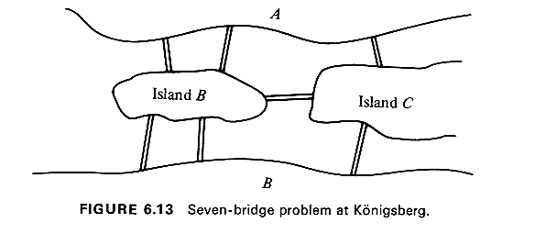
The Chinese postman's problem (CPP) has an interesting history. It was examined in detail for the first time by the great Swiss mathematician and physicist Leonhard Euler in the eighteenth century. Euler tried to find a way in which a parade procession could cross all seven bridges shown in Figure 6.13 exactly once. These seven bridges were at the Russian city of Konigsberg (now Kaliningrad) on the river Pregel. Euler proved in 1736 that no solution to the Konigsberg routing problem exists. He also derived some general results that provide the motivation for the solution approaches to the CPP that have been devised recently. At this time, efficient (i.e., polynomial time) algorithms exist for solving the CPP on undirected graphs and on directed graphs. Interestingly, a solution approach to the CPP on directed graphs (which, incidentally differs in important respects from the corresponding approach in the case of undirected graphs) was developed in the course of a project aimed at designing routes
for street-sweeping vehicles in New York City [BELT 74]. After several
researchers had spent a good amount of time trying to develop a similarly
efficient procedure for solving the CPP on a mixed graph, it was
finally shown [PAPA 76] that this last problem belongs to a class of very
hard ("NP-complete") problems for which it is unlikely that polynomial
algorithms will ever be found (see also Section 6.4.6)!
10 On the other hand, the mailman might instead wish to minimize the number of "pound miles" per day. This may result in a distinctly different route. 11 The name derives fromt the fact that an early paper discussing this problem appeared in the journal Chinese Mathematics (MEI 52). |