


6.4.3 Obtaining an Euler TourLet G(N, A) be a connected graph with no nodes of odd degree. Then an Euler tour can be drawn on G in the following manner. Euler-Tour Algorithm (Algorithm-6.4) Begin at any desired starting node n0
Algorithm 6.4 is very simple and convenient for manual applications. However, it is not particularly well suited for computer solutions. Whereas it is a trivial task for a human being to decide at each point whether a particular edge is or is not an isthmus, this is a time-consuming procedure for a computer. For that reason, alternative algorithms for obtaining Euler tours have been suggested for computer implementation. One of these algorithms, as we have already mentioned, is based on the procedure outlined in our earlier proof of Euler's theorem.
From the description of Algorithm 6.4 it is clear that, in most cases,
there exist many different Euler tours for any connected G(N, A) with no
nodes of odd degree, in the sense that the routes followed in traversing all
the edges of G are different However, all Euler tours of any given graph
naturally have the same total length, equal to
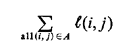
The application of Algorithm 6.4 to finding an Euler path for graphs with two odd-degree nodes is also straightforward (one simply starts from one of the odd-degree nodes and ends up at the other). |