


6.4.6 Solving TSP1We shall now present a heuristic algorithm for TSP1 [CHRI 76]. The algorithm consists of three major steps, each of which, in turn, consists of the application of other well-known algorithms that we have already discussed. A fourth step, which usually offers further improvements in the solution, can be easily added to the procedure and will be described separately. The basic three steps of our heuristic algorithm produce a tour that is guaranteed to be less than 50 percent longer than the optimal tour. Although this may not sound particularly exciting, it turns out that this is the best "worst-case performance" achieved by any efficient TSP algorithm devised so far. Consider n points that must be traversed by a TSP1 tour (symmetric distances, complete connectivity, triangular inequality). Then we have: Heuristic Algorithm for TSP1 (Algorithm 6.6)
Let us now pause to consider the characteristics and properties of the TSP solution whose derivation we just described. It should first be clear that the solution does indeed have the two properties of a traveling salesman tour that we specified earlier: namely, it is a circuit--beginning and ending at the same (specified or not) node--and it does visit each and every node at least once since it is an Eulerian circuit that covers all links of the Anode graph H that we have created. What is now the relationship between the length of the tour that we have just obtained (i.e., the length of H) and the length of the actual optimum traveling salesman tour ? Although we have not found the optimum solution to the TSP, we can still place a bound on how far our solution can deviate from the optimum solution in the following way. Let us denote by L(H), L(T), L(M), and L(TST) the length of H. T. and M,
as defined, and of the (unknown) optimum traveling salesman tour,
respectively.
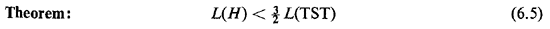
Proof: Suppose, for the moment, that somehow we have
managed to obtain the optimum traveling salesman tour (TST). Since the TST
is a circuit that covers all n points and visits each exactly once, it is
clear that if we remove any one of the links on the TST, what will be left
will be a spanning tree (not necessarily the minimum one) with n nodes and
n - 1 links. Since T. by definition, is the minimum spanning tree, and since
all distances are positive, it then follows that

In a similar vein, suppose that we took the TST and identified on it the
n o points that were optimally matched in Step 2 of our algorithm.
Suppose that we then matched pairwise, in an optimum manner, these
no nodes by using only links that are contained in the TST.
Let the set of all links used in this matching be denoted as M'. For the
length of the subgraph M', L(M'), it must then be true that

For were this not so, M' could not possibly be the minimum length matching in TST of the n0 nodes. At the same time, however, it is obvious that L(M) 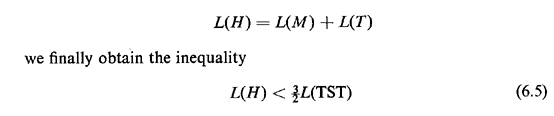
A fourth step, which can further improve the solution obtained at the end of Step 3, can also be added to Algorithm 6.6:
For instance, if the tour at the conclusion of Step 3 reads, partly, as {A, B. C, D, B. E, . . .} where each capital letter represents a distinct point, we can consider improving the tour by using either the sequence {A, C, D, B. E, . . .} or {A, B. C, D, E, . . .}. Note that Step 4 can be easily performed in O(n2) t--or even faster if one is careful. Since the three basic steps of Algorithm 6.6 also involve three efficient algorithms, the whole algorithm is efficient as well, and can be performed in O(n3) time. (Why?) Finally, while Algorithm 6.6 can lead to solutions that are as much as 50 percent worse than the optimal, practical experience has shown that in applications involving tours with more than 50 or so points, the algorithm rarely gives solutions that are more than 10 percent worse than the optimal (provided that the points have not been prearranged so as to "defeat" the algorithm). In fact, the performance of Algorithm 6.6 can usually be expected to improve as the number of points, n, increases. On the other hand, it is possible to find "pathological" examples for which the worst-case performance is indeed attained asymptotically. Exercise 6.6 Argue that for the arrangement of points shown in Figure 6.20, the solution given by the first three steps of Algorithm 6.6, approaches 3/2 · L (TST) as m increases. (Assume that e << 1.) note that, for m = 1, algorithm 6.6 gives the optimal tour. 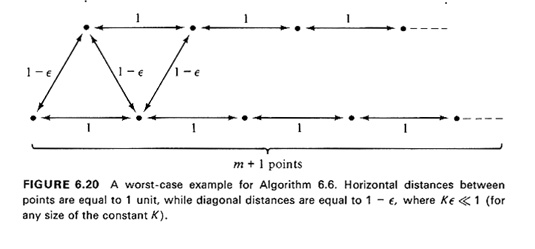
We now illustrate the application of Algorithm 6.6. Example 9: Refuse-Collection Tour 
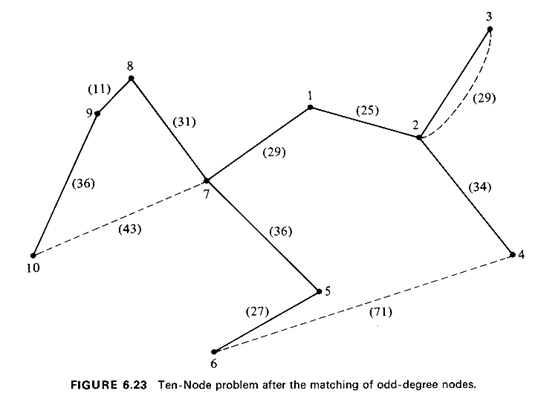
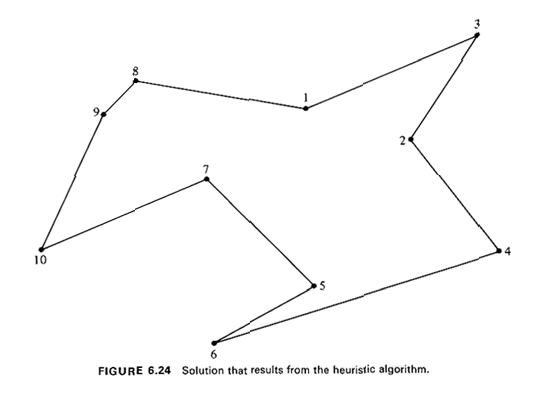
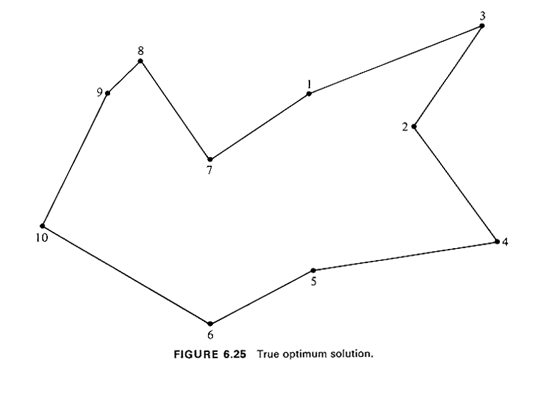
16 This is a simplified version of a problem actually encountered in Brookline, Massachusetts by a colleague of the authors. |