


Problems6.1 Shortest paths with some (i, j) < 0 when some link
lengths on a network are negative the two shortest-path algorithms of
section 6.2 must be modified. algorithm 6.1 must be modified drastically,
while only a minor modification is necessary in algorithm 6.2. in this
problem we shall explore various aspects of the shortest-path problem with
some
(i, j) < 0 when some link
lengths on a network are negative the two shortest-path algorithms of
section 6.2 must be modified. algorithm 6.1 must be modified drastically,
while only a minor modification is necessary in algorithm 6.2. in this
problem we shall explore various aspects of the shortest-path problem with
some  (i, j) < 0. (i, j) < 0.
6.2 Intersection of two-way streets Consider the intersection of two major avenues near the center of a city. The intersection is controlled by a set of traffic lights. Both avenues carry two-way traffic. Cars wishing to make a right turn at the intersection incur a "penalty" of two time units; those making a left turn, a penalty of four time units; and those continuing on a straight course, a penalty of one time unit. No U-turns are permitted. Draw a network model of this intersection. The model should be a finest-grained one, so that all possible actions of motorists at this intersection can be accounted for. 6.3 Network model of commuter's choices In the case shown in Figure P6.3, a commuter wishes to travel from his residence near station A to his place of employment at D. The commuter's transportation choices are:
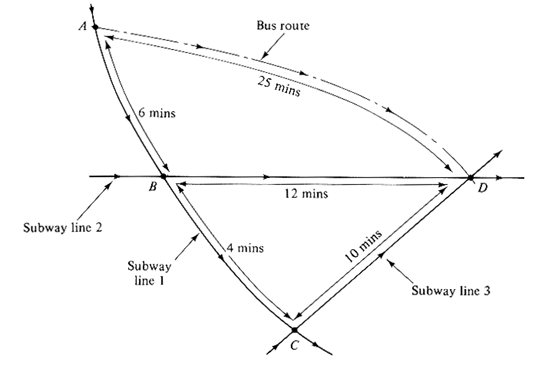
Headways between subways on all lines are exactly 10 minutes. Moreover, the subway schedules are coordinated so that a line 2 train to D passes through B exactly 4 minutes after a line 1 train has stopped at B. and similarly, a line 3 train to D passes through C exactly 4 minutes after a line 1 train has stopped at C. Assume that transfer times and stop time are negligible. Headways between buses at A are also constant and equal to 10 minutes.
6.4 Design of an optimum road network Suppose that in Figure 6. 11, the nodes of the graph represent seven towns in a rural area and its links a set of paved roads which could possibly be constructed to connect the towns. Note that some connections (e.g., C to D) cannot be built (owing, perhaps, to such constraints as mountainous terrain). The distances indicated on Figure 6.11 are miles. Suppose now that a regional commission charged with planning the road
network in this area: (1) has a budget sufficient to construct up to a total
of 34 miles of paved roads; and (2) wishes to minimize the quantity
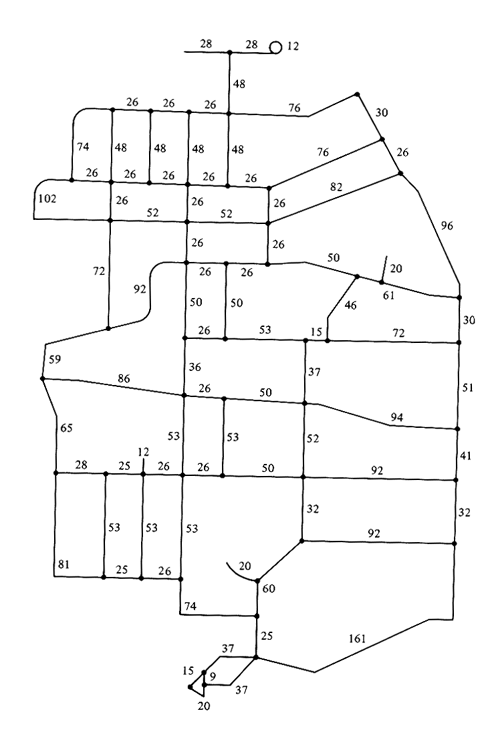
Z = Find the optimum road network for this case. (This is an example of "optimum network design," a class of difficult network problems.) 6.5 Solving the CPP on a city map It has been pointed out that good solutions to urban Chinese postman problems can usually be found quite easily, even for large networks, if a good map is available. The map of Figure P6.5 involves about 50 nodes and 90 arcs. It is based on a test problem due to P. Authier (University of Sherbrooke, Canada). There are 38 odd-degree nodes in the network (i.e., more than 1021 alternative matchings)! Solve the CPP for this network using Algorithm 6.5 and finding a matching of odd-degree nodes by inspection (plus trial and error). Make a photocopy of the map and indicate (by doubling lines in red pencil or in ink) the street segments that must be traversed twice in your solution. (A tour is required; distances are in tens of feet.) What is the total distance that will be traversed twice in your solution ? (In the optimal solution the answer is 8,360 feet, including the length of dead-end street-- which must be traversed twice anyway.) 6.6 Chinese postman problem on a directed network To solve
the CPP on a directed network [BELT 74], we begin by quoting the version of
Euler's theorem that applies to directed networks:
A connected directed network possesses an Euler tour if and only if the indegree and the outdegree of every one of its nodes are equal. The proof of this theorem is completely analogous to the proof of Euler's theorem for undirected networks (you may wish to retrace its steps). To solve the CPP on any directed graph, we first define
A node i for which Pt > O (Pi < o) is called
a "supply" ("demand") node. we indicate the sets of supply and demand nodes
as s and d, respectively.
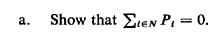
The following algorithm solves the CPP on directed graphs (the algorithm is stated informally):
6.7 Upper bound on the expected length of the TST A total of n points are randomly and uniformly distributed within a unit square. We wish to obtain an upper bound on the expected length of the optimum traveling salesman tour, E[TST], through these n points. Suppose that we divide the unit square into m equal-width columns, as shown on Figure P6.7, where m is to be determined later. We visit all n points through the following strategy. We start from the point in the leftmost column having the largest y coordinate. We then visit the point in the same column having the next lower y coordinate, and so on. When we reach the lowest point in the first column, we next visit the lowest point in the second column and we then traverse the points in that column upward. We continue this process by visiting all columns from left to right, changing the direction of traversal at each column. To complete the tour, we join the last point to the first point with a straight line. Let Sn be a random variable denoting the length of this tour.
Clearly, E[Sn]
6.8 Coin collection from parking meters Figure P6.8 shows a section of a downtown area. A special coin-collection truck must traverse all street segments indicated with solid lines once a week, to collect coins deposited in parking meters by motorists. Parking meters exist on only one side of these streets. Street segments indicated by dashed lines do not have parking meters and therefore need not be traversed, except as necessary to travel between parts of the downtown street grid. Travel in all street segments is permitted in only one direction, as indicated by the arrows in Figure P6.8. An east-west block is 9 units long, and a north-south block is 6. Diagonal street segments are 11 units long. Note that there is no direct connection between points 3 and 7. What is the length of the shortest route that the truck can travel
beginning and ending at point 1 and traversing, at least once, all street
segments with parking meters? Describe one such shortest route.
How is this problem different from the CPP on directed networks? Can you devise a systematic procedure for dealing with this family of problems ? 6.9 Proof of Hakimi's theorem Prove that "at least one set of k-medians exist solely on the nodes of a network G" (Section 6.5.2). The proof for k = 1 was given in Section 6.5.2. 6.10 Location of a "supporting facility" Consider the network of Figure P6.10 and imagine that the nodes represent five cities, the numbers next to the nodes the "weights" of the cities, and the numbers next to the links the mile length of roadways connecting the cities. Cars travel on the roadways at an effective speed of 30 mph. Assume that a major facility, say an airport, has been located at some point on this network. A regional planning group now wishes to install a high-speed transportation link to the airport with a single station. The high-speed vehicles will travel on the network at twice the speed of cars and their route will be the shortest route to the airport. It is assumed that travelers to the airport will choose that combination of transportation modes which minimizes their access time to the airport (ignoring transfer times). To clarify the description above, assume that the airport is at node 2
and that the single station of the high-speed link is located at node 5.
Then, the access time to the airport of travelers from node 5 is 25 minutes.
However, the access time of
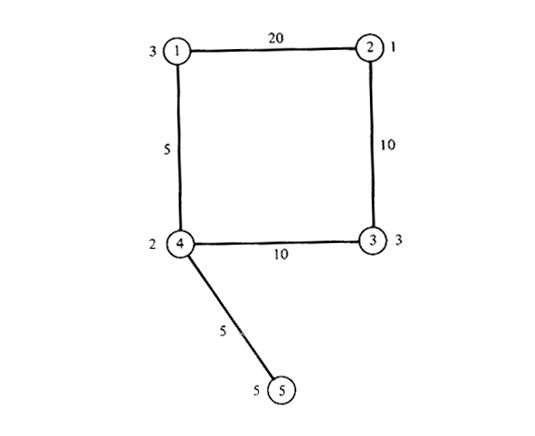
travelers from node 1 is still 40 minutes. at would take travelers from node 1 exactly 20 minutes to get to node 5 by car and then another 25 minutes to get from 5 to 2, so that it is better to go directly to the airport by car.)
It can be shown that the result you proved in part (a) holds as long as the functions f[d(x, y)] and g[d(x, y)] are both concave in d(x, y) [MIRC 79a]. 6.11 Validity of Algorithm 6.13 In this problem you are
asked to prove the validity of Algorithm 6.13 for the single center of a
tree. Using the notation of Section 6.5.4 and the symbol x* to
denote the (yet unknown) absolute center of the undirected tree network G:
and, therefore, that x* must lie on the path associated with m(es) and must be at the halfway point between es and et. |
6.12 Speeding up the search for the absolute center In our
discussion of the absolutewenter problem, it was pointed out that the quantity
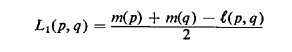
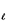 ) on a link (p, q)
[cf. (6.26)]. This bound provides a very convenient test that facilitates
the search for the absolute center of a graph.
) on a link (p, q)
[cf. (6.26)]. This bound provides a very convenient test that facilitates
the search for the absolute center of a graph.
Another bound for m(x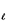 ) has been developed recently, as
follows. For the link (p, q), let r be the farthest node from p (r
) has been developed recently, as
follows. For the link (p, q), let r be the farthest node from p (r
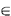 N)
and s the farthest node from q(s
N)
and s the farthest node from q(s 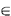 N) [i.e., m(p) = d(p, r) and
m(q) = d(q, s)]. The quantities that will be used to develop the new bound
are d(p, s) and d(q, r). Clearly, the quantity Max [d(x, r), d(x, s)]
provides a lower bound on m(x
N) [i.e., m(p) = d(p, r) and
m(q) = d(q, s)]. The quantities that will be used to develop the new bound
are d(p, s) and d(q, r). Clearly, the quantity Max [d(x, r), d(x, s)]
provides a lower bound on m(x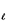 ).
).
| a. | Prove the following result: The
quantity Max{d(x, r), d(x, s)} may attain at most a single local minimum
within (q, p), i.e., excluding the nodes p and q. If such a local
minimum exists it is attained at a point x0 E (p, q) which is
a distance
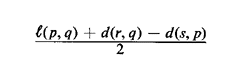
away from node p along (p, q) and at which the value of Max{d(x, r),
d(x, s)} attains the value
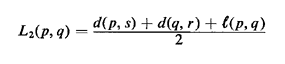
L2(p, q) is then a lower bound for m(x |
| b. | Show that L2(p, q) 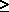 L1(p, q), that is, that L2(p, q) provides a better
lower bound and thus a sharper test than L1(p, q) for speeding up
the search for the absolute center of a graph.
L1(p, q), that is, that L2(p, q) provides a better
lower bound and thus a sharper test than L1(p, q) for speeding up
the search for the absolute center of a graph.
|
6.13 Facility location with congestion The network of Figure P6.13 represents five towns and the roadways connecting them. Emergency medical centers (one or more) are to be located in this area. The numbers in parentheses indicate the average number of calls for assistance generated per hour at each of the five towns. For each town the call-generating process can be considered Poisson and the process for each town is independent of that for all others. The numbers on the links of the network indicate the travel time, in minutes, for ambulances traveling that link (we assume that travel times within the towns are equal to 0).
Assume that it has been decided to locate exactly two medical facilities in this region. Each medical facility will be assigned a set of towns that it will serve exdusively (the two sets are mutually exclusive and collectively exhaustive). Once the two sets of towns have been determined, the two facilities will operate as separate and independent entities. Each facility operates in the following way.
Ambulances are stationed at each medical facility and travel to incidents
(and back) along shortest paths.
Once a call for service is received, and provided that an ambulance is available, an ambulance is immediately dispatched to the caller. The ambulance spends exactly 4 minutes at the scene of the call for all calls and then travels back to the medical facility (travel takes exactly the same time both ways). As soon as an ambulance returns to its origin, it immediately becomes available to respond to the next call.
Calls for service that are received when no ambulances are available are placed in a first-come, first-served queue and eventually receive service. No calls for service are ever lost.
| a. | Show that if it is desired to minimize the average service time on this network (where a service time consists of the round trip travel time plus the time spent on the scene) the two separate medical facilities should be placed at two nodes of the network. |
| b. | The optimal locations of the two facilities have now been determined with the objective of part (a) in mind. Determine the minimum number of ambulances to be placed at each one of the two facilities if the whole system (i.e., the ambulance dispatching process from the two centers) is ever to reach steady state. (The minimum number need not be the same for both facilities.) Please explain your work and reasoning clearly. |
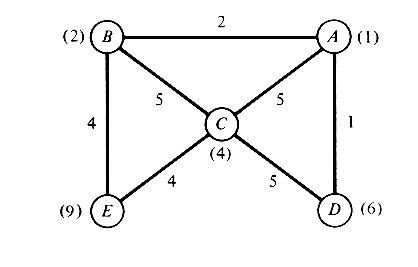
| c. | How would your answer to part (b)
change if the duration of time spent on the scene of each call for service
were, instead, a random variable S, with pdf
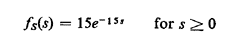
where S is given in hours? Please explain your answer. |
6.14 Review of several problems Figure P6.14 shows a transportation network with 10 demand points (towns, centers, etc.)
| a. | What is the location of an emergency facility that minimizes expected travel time? |
| b. | A regional planning committee wishes to designate "emergency artery" roads so that all the demand points are connected in time of snow. If the criterion is to select the minimum total length (in terms of travel time) of emergency artery roads, what are the corresponding roads? |
| c. | What is the median and the absolute
center with respect to the emergency artery roads only?
|
| d. | Note that nodes E, G, C, and F are demand points with large demand rate. By inspection, determine the minimum network (subgraph) that connects these points. |
| e. | How will the solution in part (d) change if J is also included in the required subgraph ? |
| f. | Comment on the answers of parts (d) and (e). Is there any special network structure for these subgraphs? |
| g. | Find a "good" traveling salesman tour on this graph. (Your tour need not be optimal and you may use any approach you wish.) |
| h. | What is the length of the optimum Chinese postman tour of this network? |
6.15 Multiple delivery routes The circulation manager of a small newspaper in a town is asked to reorganize the delivery of the newspaper. The travel network is shown in Figure P6.15.
The newspaper is produced at node 2 and must be delivered to all the other
nodes. The manager should decide how many people must be hired to distribute
the newspaper. In order to maximize service, the longest of all routes should
be as short as possible, but in order to minimize costs the total length of
the routes of all people delivering the newspapers should be as short as
possible too. These two goals are, in general, contradictory! (Explain why.)
The circulation manager meets the goals in the following way:
For all reasonable numbers of hired people he computes the routes such that the total length of the routes is minimized and each hired person has a route of nonzero length. He now compares the length of the longest route for the different solutions with different numbers of hired people. He then chooses the number of people N to hire, such that the longest route with N people is less than with N - 1 people, but is equal to the longest route with N + 1 people. What number is N?
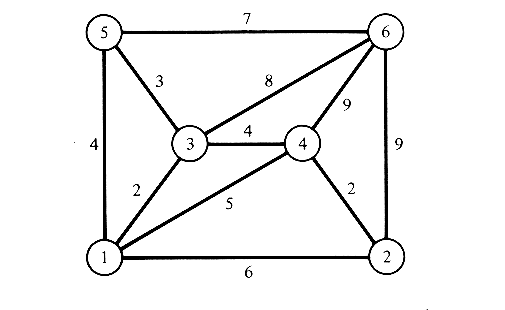
6.16 Design of an optimum road network considering congestion It is well-known that travel time by car depends on the number of other cars on the same road. Keeping this in mind, let us consider the following simple problem.
We are given the network of Figure P6.16 where the travel time from node
i to j, namely cij, depends on the flow (number of cars per unit
time) x on that arc. Let:
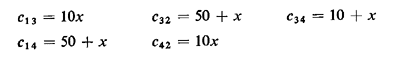
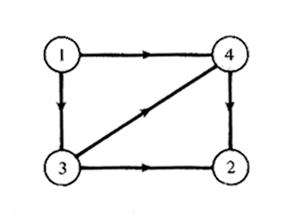
We now send a flow of 6 cars per unit time from node 1 to node 2.
| a. | As each driver tries to minimize his
travel time independently from the other drivers, all possible routes
(namely 1-3-2, 1-3-4-2 and 1-4-2) will have a flow density such that the
route lengths (travel times) are equal. (Why?) Knowing this, how much flow
will be on each arc and what is the travel time for all drivers ?
|
| b. | Assume now that someone, perhaps a police officer, is regulating the traffic. This means the police decide how much flow is allowed on each arc. Is it possible to regulate the traffic such that the travel time for every driver is lower than it was before, when each driver decided on his own? (The answer is yes!) How should the traffic be apportioned ? |
| c. | If the arc from node 3 to 4 did not exist and you were to decide if it should be built, what would you recommend? |
6.17 Facility location with queueing Consider two small towns which are one unit distance apart, as shown in Figure P6.17. (Each town is represented as a single point (node) on this simple "network," i.e., intra-town distances can be considered insignificant).
A hospital equipped with a single ambulance is located at some point between the two towns which is a distance x away from the halfway point between the two towns.
Calls from the two towns that require dispatching of the ambulance occur
in a Poisson manner at a combined rate 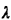 = 1/4 calls/unit time. A
fraction fA of these calls come from Town A and a fraction
fBfrom Town B (fA + fB = 1)
= 1/4 calls/unit time. A
fraction fA of these calls come from Town A and a fraction
fBfrom Town B (fA + fB = 1)
In responding to each call the ambulance travels to the appropriate city
at a constant speed v, spends a constant amount of time 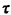 on the scene
(picking up a patient) and returns to the hospital (with the patient) at the
same constant speed v. Let v = 1 distance unit/time unit and
on the scene
(picking up a patient) and returns to the hospital (with the patient) at the
same constant speed v. Let v = 1 distance unit/time unit and 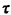 = 1 time unit.
= 1 time unit.
Calls for ambulance dispatching queue up in a first-come, first-served manner until the ambulance eventually serves them. We define the "total response time" of the ambulance to a patient as the time interval between the instant when that patient calls for the ambulance and the instant when the patient arrives at the hospital.
| a. | Assuming steady-state conditions,
find the expected total response time to a random patient. Your answer
should be in terms of x, fa and fb only.
Hint: To keep the algebra simple, write your answer in terms of
x and of (fa - fb).
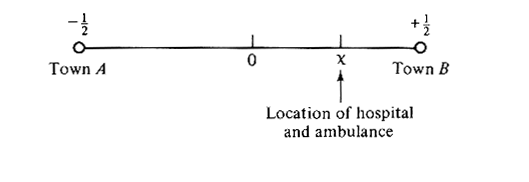
|
| b. | If the objective is to minimize the expected total response time per patient, what is the optimal value of x when fa = fb = 1/2? |
| c. | Does your answer in (b) agree with or violate Hakimi's theorem for the location of a median on networks? Please explain briefly. |
| d. | In the general case
(arbitrary 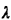 , , 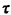 , v, fa and fb), does the question of
whether steady-state is reached depend on the location of the
hospital/ambulance? Please explain briefly (no mathematics).
, v, fa and fb), does the question of
whether steady-state is reached depend on the location of the
hospital/ambulance? Please explain briefly (no mathematics).
|
| e. | Suppose now that all calls that find
the ambulance busy, i.e. away from the hospital, are lost (e.g., the
patients are transported to the hospital by taxi). Where should the hospital
be located in this case if fa = 0.8 and fb = 0.2
(and, as before, 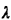 = 1/4, = 1/4,
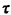 = 1, v = 1) and the objective is still to
minimize expected total response time for those patients who are served
by ambulance? (Note that no queueing ever occurs in this case.) = 1, v = 1) and the objective is still to
minimize expected total response time for those patients who are served
by ambulance? (Note that no queueing ever occurs in this case.)
|
| f. | Repeat part (e) assuming that an additional constraint is that no total response time should ever exceed 2.6 units (induding the time on the scene). |