|
6.1 Shortest paths with some 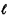 (i, j) < 0 when some link
lengths on a network are negative the two shortest-path algorithms of
section 6.2 must be modified. algorithm 6.1 must be modified drastically,
while only a minor modification is necessary in algorithm 6.2. in this
problem we shall explore various aspects of the shortest-path problem with
some
(i, j) < 0 when some link
lengths on a network are negative the two shortest-path algorithms of
section 6.2 must be modified. algorithm 6.1 must be modified drastically,
while only a minor modification is necessary in algorithm 6.2. in this
problem we shall explore various aspects of the shortest-path problem with
some 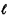 (i, j) < 0. (i, j) < 0.
| a. | Let 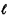 (f, e)
= -2, instead of 5, in
the graph of Figure 6.3. How would the shortest-path tree of Figure 6.5 change? (f, e)
= -2, instead of 5, in
the graph of Figure 6.3. How would the shortest-path tree of Figure 6.5 change?
| | b. | Suppose that the following approach
has been suggested for finding shortest paths on the graph of Figure 6.3
with 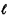 (f, e) = -2: (i) Add 2 units to the length of
all links of the graph
so that all (f, e) = -2: (i) Add 2 units to the length of
all links of the graph
so that all 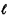 (i, j) (i, j) 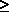 0;
(ii) use Algorithm 6.1 to find any shortest paths
required and then subtract 2 units from every link on each shortest path to
find the true length of each shortest path. What is wrong with such an
approach? 0;
(ii) use Algorithm 6.1 to find any shortest paths
required and then subtract 2 units from every link on each shortest path to
find the true length of each shortest path. What is wrong with such an
approach?
| | c. | Suppose now that
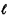 (f, e) = -8 in
Figure 6.3. What would now be the minimum distance between nodes
a and j, d(a, j) ? (f, e) = -8 in
Figure 6.3. What would now be the minimum distance between nodes
a and j, d(a, j) ?
Hint: Be careful!
| | d. | The phenomenon that you have observed
in part (c) is referred to as a "negative cycle." Whenever a negative cycle
exists between two nodes of a graph, the shortest-path problem for this pair
of nodes is meaningless. Note that this means that no undirected links
on a graph should have negative 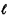 (i,j)--since this
immediately implies a
negative cycle. Shortest-path algorithms must be able to "detect" the
presence of negative cycles if they are to work with some (i,j)--since this
immediately implies a
negative cycle. Shortest-path algorithms must be able to "detect" the
presence of negative cycles if they are to work with some 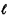 (i, j) < o. the
key to such detecting is the following statement: in a graph with n nodes,
no meaningful shortest path (i.e., one that does not indude a negative cycle)
can consist of more than n - 1 links. argue for the validity of this statement.
(i, j) < o. the
key to such detecting is the following statement: in a graph with n nodes,
no meaningful shortest path (i.e., one that does not indude a negative cycle)
can consist of more than n - 1 links. argue for the validity of this statement.
| | e. | Algorithm 6.2 can be used as stated
for cases where some 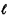 (i, j) < o with only a minor
modification to check
for the existence of negative cycles upon termination. how would you use
the final matrix d(n) at the conclusion of Algorithm 6.2 to
check whether there are any negative cycles in a graph? (i, j) < o with only a minor
modification to check
for the existence of negative cycles upon termination. how would you use
the final matrix d(n) at the conclusion of Algorithm 6.2 to
check whether there are any negative cycles in a graph?
Hint: What should happen to one or more diagonal elements
dn(i, i) of this matrix if there is a negative cycle in the
graph ?
| | f. | Repeat Example 2 of Section 6.2.2
for the case in which the length of the directed arc from node 5 to node 2
in Figure 6.6 is equal to -3.
| | g. | Can you suggest how shortest-path
Algorithm 6.1 should be changed in order to be applicable to cases with
some 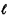 (i, j) < 0? (i, j) < 0?
Hints: No labels can become permanent (i.e., nodes cannot become
closed) until all labels are permanent; the algorithm requires at
most N - 1 passes but may terminate earlier if no labels change
during a pass.
| | For a more extensive discussion of algorithms of this type,
see, for instance, Chapter 8, Section 2.2, of Christofides [CHRI 75].
|
|


